Mnożenie pisemne
Jak mnożyć pisemnie liczby? Mnożenie pisemne liczb wielocyfrowych lub ułamków dziesiętnych wykonujemy w słupku, zapisując liczby pod sobą, równając do prawej (do liczby jedności). Następnie mnożymy przez siebie wszystkie cyfry, zapisując wyniki pod kreską. Dodając wyniki tego mnożenia, otrzymamy iloczyn szukanych liczb.
Przykłady
A oto dwa przykłady pisemnego mnożenia liczb:

Mnożenie pisemne ułamków dziesiętnych
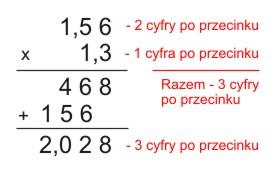
Podobnie postępujemy przy mnożeniu ułamków dziesiętnych, czyli omówimy mnożenie pisemne z przecinkiem. Liczby zapisujemy tak, aby były wyrównane do prawej kolumny. Po prawidłowym zapisie liczb w słupku dokonujemy mnożenia według opisanej wyżej za pomocą animacji procedury, a następnie liczymy, ile cyfr w obu (łącznie) liczbach znajduje się po przecinku i stawiamy przecinek w iloczynie tak, aby liczba cyfr po przecinku była taka sama.
Przykłady
Warto jeszcze wspomnieć o mnożeniu sposobem pisemnym liczb, będących wielokrotnością liczby 10. Możemy w tym przypadku pomijać „końcowe” zera (wyrównujemy do prawej kolumny jedynie cyfry różne od zera). Wykonujemy pisemne mnożenie, nie biorąc pod uwagę zer spoza prawej, skrajnej kolumny i do wyniku dopisujemy tyle zer, ile ich pominęliśmy w zapisie. Najlepiej zilustruje to przykład:
Przykłady

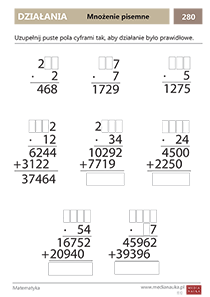
Poniżej znajdziesz karty pracy. Znajdziesz tu przykłady mnożenia pisemnego do druku. Karty pracy obejmują mnożenie pisemne przez liczby jednocyfrowe, mnożenie pisemne przez liczby dwucyfrowe i możenie pisemne przez liczby wielocyfrowe. Są tu zadania polegające na wykonaniu samodzielnie mnożenia, a także zadania typu „uzupełnij mnożenie pisemne”.
Zadania z rozwiązaniami

Zadanie nr 2.
Wykonaj mnożenie pisemne:
a) 75,4∙12,5
b) 2,37∙0,82
c) 1,253∙2,4
Wybrane karty pracy
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-01-07, A-129
Data aktualizacji artykułu: 2023-03-06


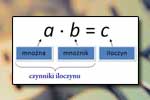 Iloczyn
Iloczyn Tabliczka mnożenia
Tabliczka mnożenia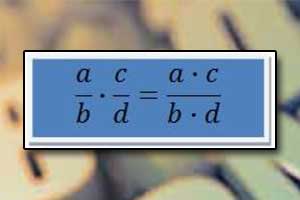 Mnożenie ułamków zwykłych
Mnożenie ułamków zwykłych Symbol Pi
Symbol Pi Dzielenie pisemne
Dzielenie pisemne