Okrąg opisany na trójkącie
Okrąg opisany na trójkącie (wielokącie) jest to okrąg, na którym leżą wszystkie wierzchołki tego trójkąta (wielokąta).
Poniższy rysunek przedstawia okręgi opisane na trójkącie i czworokącie oraz pięciokącie foremnym.
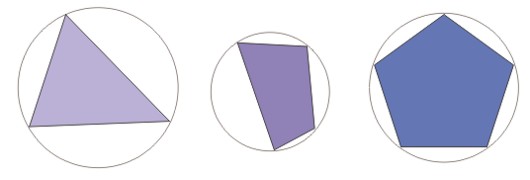
Jeśli okrąg opisany na wielokącie jest brzegiem koła, to takie koło nazywamy kołem opisanym na wielokącie, wielokąt zaś — wielokątem wpisanym w to koło.
Twierdzenie
Trzy symetralne boków trójkąta przecinają się w jednym punkcie — środku okręgu opisanego na tym trójkącie.
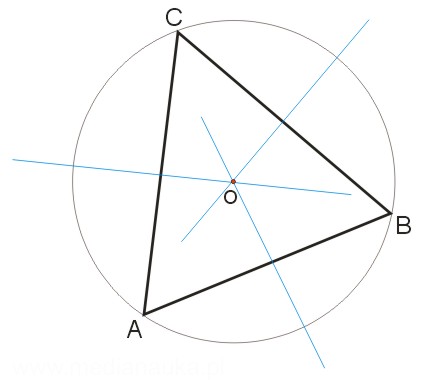
Na każdym trójkącie można opisać okrąg. Należy jednak pamiętać, że nie na każdym wielokącie można opisać okrąg. Jeśli można, środek okręgu jest punktem przecięcia symetralnych boków wielokąta.
Konstrukcja okręgu opisanego na trójkącie
Konstrukcja okręgu opisanego na trójkącie sprowadza się do konstrukcji trzech symetralnych boków trójkąta. W ten sposób wyznaczamy środek okręgu. Promień okręgu leży na prostej łączącej środek okręgu z dowolnym wierzchołkiem trójkąta. Konstrukcję okręgu wpisanego w trójkąt można prześledzić na poniższym filmie.
Poniższy film pokazuje jak narysować okrąg opisany na trójkącie.
Okrąg opisany na trójkącie — wzory
Okrąg opisany na trójkącie równobocznym
Przedstawiamy wzór na promień okręgu opisanego na trójkącie równobocznym o boku długości a:
Okrąg opisany na trójkącie prostokątnym
Trójkąt oparty na średnicy jest prostokątny.
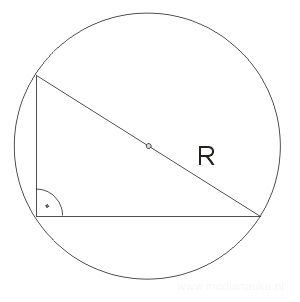
Konstrukcja okręgu opisanego na trójkącie prostokątnym sprowadza się więc do wyznaczenia środka odcinka przeciwprostokątnej.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami
Zadanie nr 1.
Znaleźć środek okręgu opisanego na trójkącie \(ABC\), gdzie \(A=(2,0), B=(1,2), C=(-2,-1)\).
Inne zagadnienia z tej lekcji
Okrąg wpisany w trójkąt
Okrąg dopisany do trójkąta
Okrąg opisany, do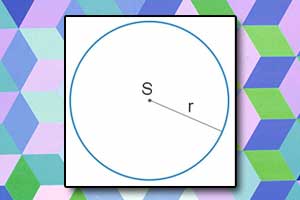pisany i wpisany w trójkąt
Okrąg i koło
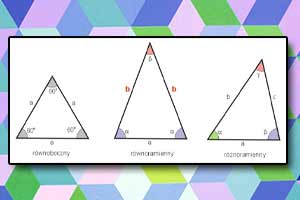Trójkąty© medianauka.pl, 2010-11-16, A-1019