Równanie

W niniejszym artykule określamy czym jest równanie.

Równanie z jedną niewiadomą jest to forma zdaniowa w postaci:

gdzie f, g oznaczają funkcje zmiennej rzeczywistej. Zmienną x nazywamy niewiadomą.

Przykłady równań

Oto przykłady kilku równań:

$x=5\\{x+1=0}\\{-x+1=2x+44}\\{x^3+x^4=1+x^2}\\{\sqrt{x}+1=sinx}\\{\frac{x^4-\sqrt{\frac{1}{x+1}}}{log_2{x-1}}+1=\sin{x-sqrt{1+2x}}\\{m^2+m=2m-1}$
(tutaj niewiadomą jest m).

Dziedzina równania

Dziedzina równania f(x)=g(x) jest to część wspólna dziedzin funkcji f, g.

Przykład

Jaka jest dziedzina równania $\sqrt{x}=\frac{1}{x}$ ?

Dziedziną funkcji $\sqrt{x}$ jest ${R_+}\cup{\lbrace}{0}\rbrace$ , a funkcji $\frac{1}{x}$ jest zbiór ${R\backslash}\lbrace{0}\rbrace$ . Zatem dziedziną tego równania jest zbiór liczb rzeczywistych dodatnich $R_{+}$ .

Zadanie

Znaleźć dziedzinę równania $\sqrt{x-2}=3$ .

Rozwiązanie:
$x-2\geq{0}\\{x}\geq{2}$

Odpowiedź: Dziedziną tego równania jest zbiór $\langle{2};{+\infty)}$ .

Rozwiązywanie równań

Rozwiązanie równania (pierwiastek równania) jest to każda liczba, która spełnia to równanie. Zbiór rozwiązań równania jest to zbiór utworzony ze wszystkich rozwiązań tego równania. Aby rozwiązać równanie należy znaleźć jego zbiór rozwiązań.

Przykład

Zbadajmy równanie x²-2=2.
Możemy odgadnąć, że jednym z rozwiązań jest liczba 2. Sprawdźmy to: zdanie 2²-2=2 jest prawdziwe. Ale liczba -2 też spełnia to równanie. Zbiór rozwiązań tego równania to {-2,2}.

Równania są równoważne jeżeli mają ten sam zbiór rozwiązań.
Jeżeli równanie nie ma rozwiązań (zbiorem rozwiązań jest zbiór pusty), to takie równanie nazywamy sprzecznym.
Jeżeli równanie ma nieskończenie wiele rozwiązań, to równanie takie nazywamy tożsamościowym.

Przykład

Przykład równań równoważnych: x+1=2 i x-1=0. W Obu równaniach zbiorem rozwiązań jest zbiór {1}.
Przykład równania tożsamościowego: x+1=x+1. Równanie jest spełnione dla każdej liczby rzeczywistej.
Przykład równania sprzecznego: x+1=x. Równanie nie ma rozwiązania, to znaczy nie istnieje taka liczba, która podstawiona pod niewiadomą x spełni daną równość.

Układy równań

Jeżeli liczby mają spełniać kilka równań jednocześnie, to wówczas mówimy o układach równań. Układy równań omawiamy w osobnych artykułach.

Pytania

Jak sprawdzić, czy podana liczba spełnia równanie?

Aby sprawdzić czy podana liczba spełnia równanie należy podstawić za niewiadomą tę właśnie liczbę i sprawdzić, czy równanie jest prawdziwe.

Na przykład aby sprawdzić, czy liczba 1 spełnia równanie x-1=0, obliczamy 1-1=0, co daje nam zdanie prawdziwe 0=0. Liczba 1 spełnia więc nasze równanie.

Jak rozwiązać równanie?

Trzeba znaleźć taką wartość niewiadomej, dla której równanie jest prawdziwe. Teoretycznie można odgadnąć wartość x. Na przykład od razu można odgadnąć, że rozwiązaniem równia x-1=1 jest liczba 2, bo 2-1=1. Lepiej jednak stosować pewne metody rozwiązywania równań, gdyż mamy wówczas możliwość rozwiązania praktycznie każdego równania i mamy pewność, że znaleźliśmy wszystkie rozwiązania.

Poniżej przedstawiamy linki do artykułów, w których pokazujemy jak rozwiązujemy różne typy równań:

Ile rozwiązań ma równanie?

Czasami równanie nie ma rozwiązań (na przykład x²+1=0). Czasem ma ich nieskończenie wiele (na przykład x+1=2x+2). Równanie może mieć jedno lub wiele rozwiązań.

Co to jest pierwiastek równania?

Pierwiastek równania to inaczej jego rozwiązanie.

Co to jest równanie tożsamościowe?

Równanie tożsamościowe jest to takie równanie, które ma nieskończenie wiele rozwiązań. Podstawienie pod niewiadomą dowolnej liczby powoduje otrzymanie równania prawdziwego. Przykłady równań tożsamościowych: x=x, x+1=2x+2.

Co to jest równanie sprzeczne?

Równanie sprzeczne jest to takie równanie, którego nie spełnia żadna z liczb rzeczywistych. Przykłady równań sprzecznych: x²+1=0, √x=-1, 1/x=0.

Zadania z rozwiązaniami

Zadania związane z tematem:
Równanie

Zadanie - dziedzina równania
Znaleźć dziedzinę równania:
$x=\frac{1}{\sqrt{x}}$
b) $\frac{x}{2x+1}=\frac{1}{x^2-4x+4}$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Nierówność
Nierówność - wiadomości podstawowe

Rozwiązywanie równań
Metoda równań równoważnych polega na przekształcaniu równania w taki sposób, aby każde kolejne było równoważne danemu i łatwiejsze do rozwiązania.

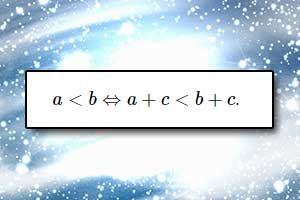Rozwiązywanie nierówności
Metoda nierówności równoważnych polega na ich przekształcaniu w tak, aby każde kolejne było równoważne i łatwiejsze do rozwiązania.

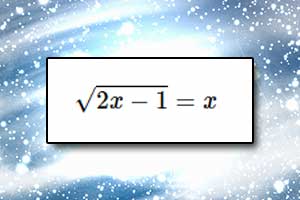Metoda analizy starożytnych
Metoda analizy starożytnych polega na przekształcaniu równania tak, aby otrzymać równanie łatwiejsze i spełniające rozwiązania równania wyjściowego.

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.