Wykres funkcji liniowej
Wykresem funkcji liniowej jest prosta.
Jak narysować wykres funkcji liniowej? Wystarczy więc wyznaczyć dwa punkty, przez które ona przechodzi. Zwykle są to punkty przecięcia prostej z osiami układu współrzędnych.
Punkt przecięcia prostej o równaniu \(y=ax+b\):
- z osią OY: \((0,b)\),
- z osią OX: \((-\frac{b}{a},0)\).
Przykłady
Narysuj wykres funkcji liniowej o równaniu \(y=2x-4\).
Współczynnik kierunkowy \(a=2\), a wyraz wolny \(b=-4\). Sporządzamy tabelkę wartości funkcji(wystarczą dwa punkty):
| \(x\) | \(0\) | \(-\frac{b}{a}=-\frac{-4}{2}=2\) |
| \(y\) | \(b=-4\) | \(0\) |
Sporządzamy na podstawie tabelki wykres (zaznaczamy w układzie współrzędnych punkty \((0,-4)\) oraz \((2,0)\) i prowadzimy przez nie prostą).
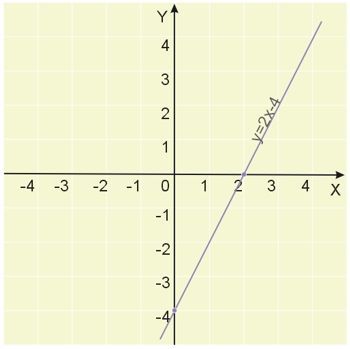
Aby wykreślić wykres funkcji liniowej, możemy obrać sobie dowolne punkty (argumenty funkcji) i obliczyć dla nich poprzez wstawienie do wzoru funkcji wartości funkcji.
Równanie kierunkowe prostej
O równaniu \(y=ax+b\) mówimy, że jest to równanie (kierunkowe) prostej w układzie współrzędnych.
Każda prosta w układzie współrzędnych nierównoległa do osi OX jest opisana równaniem \(y=ax+b\). Natomiast prostą równoległą do osi OY opisujemy równaniem \(x=c, {c}\in \mathbb{R}\).
Ciekawostki
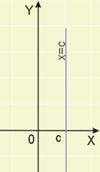
Dlaczego prosta równoległa do osi OY nie może być opisana za pomocą funkcji liniowej?
Odpowiedź jest dość prozaiczna. Otóż prosta równoległa do osi OY nie jest wykresem żadnej funkcji! Pamiętamy, że funkcja jest to przyporządkowanie każdemu elementowi z pewnego zbioru dokładnie jednego elementu z innego zbioru. Tutaj jednak jednemu elementowi (liczbie \(c\)) przypisujemy nieskończenie wiele elementów.
Mimo że nie mamy tutaj do czynienia z wykresem funkcji, nie przeszkadza to zapisaniu równania prostej. Ponieważ wszystkie punkty prostej mają tę samą współrzędną \(x\), możemy zapisać równanie prostej w postaci \(x=c\).
Kąt nachylenia prostej
Współczynnik kierunkowy prostej ma wpływ na kąt nachylenia prostej do osi OX układu współrzędnych. Otóż współczynnik ten jest równy tangensowi kąta nachylenia prostej do osi OX.
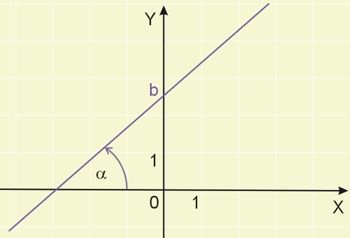
Im większy jest współczynnik \(a\), tym większy kąt nachylenia (bardziej stroma prosta). Ilustruje to poniższy rysunek:
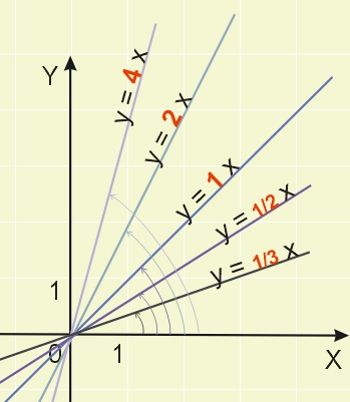
Na położenie prostej w układzie współrzędnych ma wpływ także wyraz wolny. Wyraz wolny \(b\) decyduje o tym, w jakim miejscu prosta przecina oś OY układu współrzędnych. Im większą liczbą jest wyraz wolny, tym wyżej znajduje się wykres. Ilustruje to poniższy rysunek.
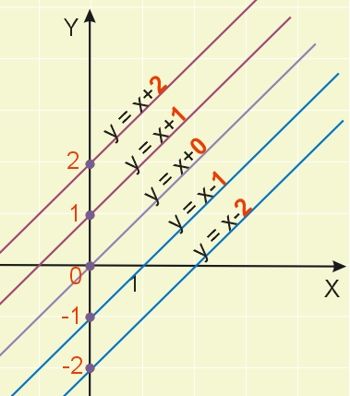
 Wykres funkcji
Wykres funkcji
Poniższa symulacja pozwala zaobserwować zachowanie się wykresu funkcji liniowej w zależności od wartości współczynników \(a\) i \(b\)
Funkcja w postaci y = ax+b, czyli y = x
a 1b 0
Miejsce zerowe x0=0
Przykłady
Do wykresu funkcji \(f\) należą punkty \(A = (0,6)\) oraz \(B=(7, -1)\). Jakie jest równanie kierunkowy tej prostej?
Rozwiązujemy układ równań, podstawiając do ogólnej postaci równania funkcji liniowej za argument i wartość funkcji współrzędne punktów A i B:
\(\begin{cases} 6=a\cdot 0 +b\\ -1=a\cdot 7+b\end{cases}\)
\(\begin{cases} b=6\\ -1=7a+6\end{cases}\)
\(\begin{cases} b=6\\ -1=7a+6\end{cases}\)
\(\begin{cases} b=6\\ -7=7a/:7\end{cases}\)
\(\begin{cases} b=6\\ a=-1\end{cases}\)
Odpowiedź: \(y=-x+6\)
Pytania
Jak narysować wykres funkcji liniowej?
Aby naszkicować wykres funkcji liniowej, wystarczy zaznaczyć w układzie współrzędnych dwa punkty i poprowadzić przez nie prostą. Jakie punkty najłatwiej wziąć pod uwagę? Proponujemy miejsce przecięcia się z osią OY (za \(x\) podstaw 0) i oblicz wartość funkcji dla dowolnej innej wartości \(x\).
Na przykład: Mając do czynienia z funkcją \(y=3x-6\), podstawmy za \(x\) liczbę zero. Otrzymujemy \(y=-6\). Mamy więc pierwszy punkt \((0,-6)\). Podstawmy teraz za \(x\) liczbę 2. Otrzymamy \(y=3\cdot 2-6=0\). Mamy więc drugi punkt \((2,0)\). Zaznaczamy oba punkty w układzie współrzędnych i prowadzimy przez nie prostą.
Jak sporządzić wykres funkcji liniowej w programie Excel?
W tabelce wpisujemy wartości danej funkcji liniowej (patrz pierwszy przykład). Po przygotowaniu danych zaznaczamy komórki arkusza w zakresie danych, a następnie wstawiamy wykres punktowy, przechodząc w menu Excela do zakładki „Wstawianie”, a następnie „Wykres punktowy” i wybieramy dowolny z nich.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 2.
Naszkicować wykres funkcji \(y=-5x+\frac{1}{2}\), określić jej monotoniczność oraz znaleźć miejsce zerowe.

Zadanie nr 3 — maturalne.
W układzie współrzędnych są dane punkty \(A=(-43,-12)\), \(B=(50,19)\). Prosta AB przecina oś \(Ox\) w punkcie \(P\). Oblicz pierwszą współrzędną punktu \(P\).

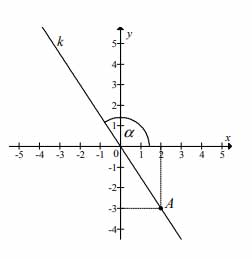
Zadanie nr 4 — maturalne.
Na rysunku przedstawiona jest prosta \(k\), przechodząca przez punkt \(A=(2,-3)\) i przez początek układu współrzędnych oraz zaznaczony jest kąt \(\alpha\) nachylenia tej prostej do osi \(Ox\).
A. \(tg\alpha = -\frac{2}{3}\)
B. \(tg\alpha = -\frac{3}{2}\)
C. \(tg\alpha = \frac{2}{3}\)
D. \(tg\alpha = \frac{3}{2}\)

Zadanie nr 5 — maturalne.
Na płaszczyźnie z układem współrzędnych proste k i l przecinają się pod kątem prostym w punkcie A = (-2, 4). Prosta k jest określona równaniem \(y=-\frac{1}{4}x+\frac{7}{2}\). Zatem prostą l opisuje równanie
A. \(y=\frac{1}{4}x + \frac{7}{2}\)
B. \(y=-\frac{1}{4}x + \frac{7}{2}\)
C. \(y=4x-12\)
D. \(y=4x+12\)

Zadanie nr 6 — maturalne.
Prosta przechodząca przez punkty \(A=(3,−2)\) i \(B=(−1,6)\) jest określona równaniem
A. \(y=-2x+4\)
B. \(y=-2x-8\)
C. \(y=2x+8\)
D. \(y=2x-4\)

Zadanie nr 7 — maturalne.
Punkty \(A=(−2,6)\) oraz \(B=(3, b)\) leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy b jest równe
A. 9
B. (-9)
C. (-4)
D. 4

Zadanie nr 8 — maturalne.
Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych \(x,y\) jednego z niżej zapisanych układów równań \(A–D\).
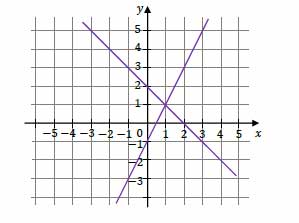
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A. \(\begin{cases} y=-x+2\\y=-2x+1\end{cases}\)
B. \(\begin{cases} y=x-2\\y=-2x-1\end{cases}\)
C. \(\begin{cases} y=x-2\\y=2x+1\end{cases}\)
D. \(\begin{cases} y=-x+2\\y=2x-1\end{cases}\)

Zadanie nr 9 — maturalne.
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji \(f\) w kartezjańskim układzie współrzędnych (x,y).
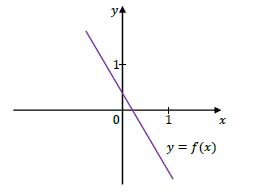
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(a\) oraz liczba \(b\) we wzorze funkcji \(f\) spełniają warunki:
A. \(a>0\) i \(b>0\)
B. \(a>0\) i \(b<0\)
C. \(a<0\) i \(b>0\)
D. \(a<0\) i \(b<0\)

Zadanie nr 10 — maturalne.
W kartezjańskim układzie współrzędnych \(x,y\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O=(0,0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(0x\), a drugie przechodzi przez punkt \(P=(-3,1)\) (zobacz rysunek).
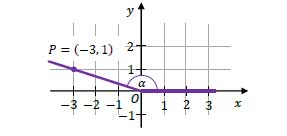
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Tangens kąta \(\alpha\) jest równy
A. \(\frac{1}{\sqrt{10}}\)
B. \((-\frac{3}{\sqrt{10}})\)
C. \((-\frac{3}{1})\)
D. \((-\frac{1}{3})\)
Powiązane quizy
Powiązane quizy
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-05-30, A-222
Data aktualizacji artykułu: 2023-04-15




 Funkcja liniowa
Funkcja liniowa Wzajemne położenie prostych
Wzajemne położenie prostych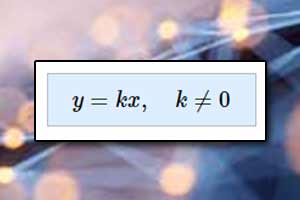 Proporcjonalność prosta
Proporcjonalność prosta