Zaokrąglanie liczb

Zaokrągleń używamy w życiu codziennym. Dla przykładu, jeżeli cena towaru wynosi 12 zł 02 gr, często powiemy, że coś kosztuje po prostu 12 złotych, uznając 2 grosze za mało istotne. Zaokrąglenia stosujemy w księgowości, kiedy musimy prawidłowo wyrazić kwotę w pełnych złotych, lub złotych i groszach, a kalkulator wynik działania podaje z dokładnością do więcej niż dwóch miejsc po przecinku. W tych i wielu innych przypadkach stosujemy ściśle określone metody zaokrąglania liczb.

Jeżeli odrzucaną cyfrą (zastępowaną zerem) jest 0, 1, 2, 3, 4, to ostatnia zachowana cyfra się nie zmienia.

Jeżeli odrzucaną cyfrą (zastępowaną zerem) jest 5, 6, 7, 8, 9, to ostatnia zachowana cyfra jest zwiększana o 1.

Przy zaokrąglaniu znak równości zmienia się na znak zaokrąglenia „≈”.

Przykłady

482,45 ≈ 482,5 ≈ 483 ≈ 480 ≈ 500.
12,8992 ≈ 12,899 ≈ 12,9 ≈ 13 ≈ 10. (pogrubioną czcionką zaznaczono przypadek, gdy ostatnią zachowaną cyfrą jest 9. Wówczas zachowana cyfra staje się zerem, a zwiększamy o jeden przedostatnią pozostałą cyfrę).
19,99 ≈ 20.
178,9899 ≈ 178,99 ≈ 179 ≈ 180 ≈ 200.
9,999 ≈ 10.

Kalkulator

Poniżej zamieszczamy prosty kalkulator — program zaokrąglający liczbę z określoną dokładnością.

Kalkulator
Podaj liczbę:

Wynik:

Cyfry znaczące

Jak widać w powyższych przykładach, zaokrąglania nie stosujemy, kiedy liczba posiada już tylko jedną cyfrę znaczącą. Cyfra znacząca jest to cyfra 1, 2, 3, ..., 9 i 0 w przypadku, gdy znajduje się pomiędzy wymienionymi wcześniej cyframi lub na końcu, gdy oznacza brak jednostek odpowiedniego rzędu. Zatem zer początkowych ani zer końcowych napisanych w wyniku zaokrąglenia lub w celu zapełnienia miejsca nie zaliczamy do cyfr znaczących.

Przykłady

Liczba 534,21 ma 5 cyfr znaczących.
Liczba 5001 ma 4 cyfry znaczące.
Liczba 5001,00 ma 4 cyfry znaczące.
Liczba 0,231 ma 3 cyfry znaczące.
Liczba 0,001 ma 1 cyfrę znaczącą.

Zaokrąglenie do N cyfr znaczących polega na takim zaokrągleniu liczby, aby w efekcie miała N cyfr znaczących.

Przykład

Dla przykładu podajemy zaokrąglenie do 5 cyfr znaczących: 4005,826 ≈ 4005,8.

Rząd liczby

Często chcemy zaokrąglić liczbę, określając jej rząd.

Jeżeli mówimy, że chcemy zaokrąglić liczbę do części dziesiątych, pozostawiamy tylko jedną cyfrę po przecinku (po zaokrągleniu), setnych części — 2 cyfry po przecinku, tysięcznych części — 3 i tak dalej.

Jeżeli chcemy zaokrąglić do pełnych dziesiątek, setek, tysięcy i tak dalej, zaokrąglamy tak, aby otrzymać liczby całkowite o minimum o 1, 2, 3, ... zerach „na końcu” po zaokrągleniu.

Przykłady

Zaokrąglenia do tysięcy:

1234 ≈ 1000.
8999 ≈ 9000.
127 635 ≈ 128 000.
78 896 ≈ 79 000.

Zaokrąglenia do setnych części:

246,445 ≈ 246,45.
0,(64) = 0,646464 ... ≈ 0,65.
154,0005 ≈ 154.
0,0191 ≈ 0,02.

Zaokrąglanie liczb dziesiętnych

Liczby dziesiętne możemy zaokrąglać z dokładnością do określonej liczby cyfr po przecinku.

Dokładność zaokrąglania	Zaokrąglenie w dół (przybliżenie z niedomiarem)	Zaokrąglenie w górę (przybliżenie z nadmiarem)
Zaokrąglanie do jedności.	1,26 ≈ 1 2,01 ≈ 2 20,3 ≈ 20	1,66 ≈ 2 2,51 ≈ 3 20,5 ≈ 21
Zaokrąglanie do dziesiątych części.	1,26 ≈ 1,3 2,01 ≈ 2,0 2,34 ≈ 20,3	1,66 ≈ 1,7 2,59 ≈ 2,6 2,05 ≈ 2,1
Zaokrąglanie do setnych części.	1,664 ≈ 1,66 2,512 ≈2,51 20,502 ≈ 20,50	1,666 ≈ 1,67 2,516 ≈2,52 20,506 ≈ 20,51
Zaokrąglanie do tysięcznych części.	1,664444 ≈ 1,664 2,51201 ≈2,512 20,5024 ≈ 20,502	1,664945≈ 1,665 2,51259 ≈2,513 20,5256 ≈ 20,525

Ciekawostki

waga

Zaokrąglenia są bardzo istotne w pomiarach różnych wielkości fizycznych i chemicznych. Zaokrąglanie polegające na określeniu liczb po przecinku, szczególnie bardzo małych wielkości, może generować względnie duży błąd. Stosuje się tutaj zaokrąglanie do liczby cyfr znaczących ( w zależności od mierzonej wielkości liczby te są różne).

Ponadto liczbę z reguły zaokrąglamy do tylu miejsc po przecinku (znaczących), aby ostatnia cyfra była pewna. Dla przykładu wynik ważenia 0,274 g na wadze o dokładności 0,001 g trzeba będzie zaokrąglić do dwóch miejsc znaczących (bo ostatnia tzn. trzecia, jest już niepewna).

Istnieje jeszcze inny sposób zaokrąglania liczb, który jest nieco dokładniejszy, ale ma zastosowanie dla dużych zbiorów liczb, otrzymywanych w wyniku różnego rodzaju pomiarów. Dla cyfr mniejszych i większych od 5 jest analogiczny do metody standardowej. Natomiast jeśli po prawej stronie zaokrąglanej cyfry znajduje się 5 i za nią kolejne cyfry, wtedy zaokrąglamy w górę: 0,3852 ≈ 0,39. Jeśli jednak 5 jest ostatnią cyfrą, wówczas zaokrąglamy tak, żeby zostawić na końcu liczbę parzystą: 0,45 ≈ 0,4; 0,35 ≈ 0,4. W szkołach tej metody nie stosujemy.

Zaokrąglanie liczb w Excelu

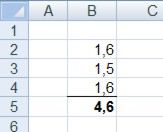
Przyjrzyj się sumie liczb z arkusza kalkulacyjnego na ilustracji. Przecież 1,6 + 1,5 + 1,6 = 4,7, a nie 4,6! Dzieje się tak wówczas, gdy w komórkach arkusza kalkulacyjnego wpisujemy liczby z większą dokładnością, niż są wyświetlane. W rzeczywistości w naszym przykładzie w komórki arkusza zostały wpisane liczby 1,55, 1,5 i 1,57 co daje wynik 4,62. Zatem po użyciu w Excelu ikony „Zmniejsz dziesiętne” ( ikonki - excel ), liczby będą wyświetlane z mniejszą dokładnością i będą zaokrąglane, jednak w pamięci komórki pozostają liczby niezaokrąglone. Zatem liczba 1,55 będzie wyświetlana jako 1,6, 1,5 jako 1,5, 1,57 jako 1,6. Sumowanie odbywa się po liczbach 1,55, 1,5, 1,57, a nie po liczbach 1,6, 1,5 i 1,6, więc otrzymany wynik 4,62, który jest zaokrąglany przy wyświetlaniu do 4,6, choć pamiętajmy, że w pamięci komórki nadal figuruje liczba 4,62.

Aby zaokrąglić liczbę w programie Excel, należy użyć funkcji "=ZAOKR()" lub kilku jej innych wersji (zobacz odpowiedzi na pytania na końcu tego artykułu).

Pytania

Jak zaokrąglać liczby w Excelu?

Korzystamy z funkcji '=ZAOKR(liczba, liczba_cyfr_po_przecinku)'. Można też skorzystać z innych funkcji arkusza kalkulacyjnego: ZAOKR.DO.CAŁK, ZAOKR.DO.NPARZ, ZAOKR.DO.PARZ, ZAOKR.DO.TEKST, ZAOKR.DÓŁ, ZAOKR.GÓRA, ZAOKR.W.DÓŁ, ZAOKR.W.GÓRĘ.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Zaokrąglanie liczb

Zadania z rozwiązaniami

Zadanie nr 1.

Zaokrąglić liczby z dokładnością do dziesiątek: 78, 37, 51, 52, 55, 99.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Zaokrąglić liczby z dokładnością do setek: 1238, 3321, 23493, 1001, 208080, 9999.

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Zaokrąglić liczby z dokładnością do setnych i dziesiątych części: 1,0909, 23,54522, 76,7452345, 9,789.

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Podaj przybliżenia dziesiętne liczb: \(\frac{1}{3}, \frac{4}{11}, \frac{5}{7}, \frac{17}{7}\) z dokładnością kolejno do dwóch, trzech, czterech i pięciu miejsc po przecinku.

Pokaż rozwiązanie zadania.