Ciągi liczbowe
Ciąg nieskończony (lub po prostu ciąg) jest to funkcja, która odwzorowuje zbiór liczb naturalnych (bez zera) w niepusty zbiór \(\mathbb{Y}\).
Wartość funkcji dla argumentu \(n\) \((n=1,2,3,...)\) oznaczamy przez \(a_n\) i nazywamy n-tym wyrazem ciągu. Ciągi liczbowe oznaczamy przez \((a_n)\) lub \((a_1,a_2,a_3,...)\).
Jeżeli wyrazami ciągu są liczby, to taki ciąg nazywamy liczbowym.
Przykłady ciągów liczbowych
Oto kilka przykładów ciągów:
- \((1,2,3,4,5...)\)
- \((2,4,6,8,16,...)\)
- \((-5,-6,-7,-8,...)\)
- \((0,2,0,3,0,4,...)\)
- \((1,\frac{1}{2},\frac{1}{3},\frac{1}{4},...)\)
Jak widać, ciąg stanowią kolejno (kolejność jest tutaj istotna) ułożone liczby według jakiegoś schematu. Schemat ten wyrażamy zwykle za pomocą wzoru.
Określanie ciągów liczbowych
W jaki sposób znaleźć wzór ciągu? Zaczniemy od przykładu.
Przykład
Wyrazić za pomocą wzoru ciąg \((2,4,6,8,...)\).
Widać, że wyrazami ciągu są liczby parzyste. Możemy więc zapisać, że n-ty wyraz ciągu wyraża się wzorem \(a_n=2n\), a sam ciąg zapisać jako \((2n)\).
Ciąg liczbowy może być określony za pomocą wzoru rekurencyjnego oraz odpowiedniej liczby wyrazów. Znaczenie rekurencji polega na odwoływaniu się funkcji do samej siebie. Oto przykład takiego określenia ciągu:
Przykład
Ciąg jest określony w następujący sposób:
\(\begin{cases}a_1=1\\a_2=3\\a_n=a_{n-2}+a_{n-1}\end{cases}\)
Powyższy wzór określa ciąg o wyrazach: \((1,3,4,7,11,...)\).
Wyrazy tego ciągu określamy, dodając do siebie dwa kolejne poprzednie wyrazy ciągu.
Aby obliczyć na przykład piąty wyraz ciągu, stosujemy wzór \(a_5=a_3+a_4\).
Ciąg skończony
Ciąg skończony jest to funkcja, która odwzorowuje zbiór \(\lbrace1,2,3,...,k\rbrace\) w niepusty zbiór \(\mathbb{Y}\).
Wartość funkcji dla argumentu \(n (n=1,2,3,...,k)\) oznaczamy przez \(a_n\) i nazywamy n-tym wyrazem ciągu. Ciąg skończony oznaczamy przez \((a_n)\) lub \((a_1,a_2,a_3,...,a_k)\).
Przykłady
Oto kilka przykładów ciągów skończonych:
- \((1,2,3,4,5)\)
- \((2,4,6,8)\)
- \((-5,-6,-7,-8,...,-100005)\)
- \((0,2,0,3,0,4,...,0,100)\)
Rodzaje ciągów liczbowych
Oto wybrane ciągi liczbowe i ich własności, które omawiamy w kolejnych artykułach:
W dalszej części lekcji omawiamy wykres ciągu liczbowego oraz jego własności.
Wzory — ciągi
W poniższej tablicy przedstawiamy przydatne wzory, związane z ciągami liczbowymi. Wzory te stanowią podsumowanie działu — ciągi liczbowe. Omawiamy je w dalszych artykułach.
| Nazwa | Wzór |
| ciąg arytmetyczny | \(a_{n+1}-a_n=r\) |
| wzór na n-ty wyraz ciągu arytmetycznego | \(a_n=a_1+(n-1)r\) |
| własność wyrazów ciągu arytmetycznego | \(a_n=\frac{a_{n-1}+a_{n+1}}{2}\) |
| suma wyrazów ciągu arytmetycznego | \(S_n=\frac{a_{1}+a_{n}}{2}\cdot{n}\) |
| ciąg geometryczny | \(\frac{a_{n+1}}{a_n}=q\) |
| wzór na n-ty wyraz ciągu geometrycznego | \(a_n=a_1\cdot q^{n-1}\) |
| własność wyrazów ciągu geometrycznego | \(a_n=\sqrt{a_{n-1}\cdot a_{n+1}}\) |
| suma wyrazów ciągu geometrycznego | \(S_n=a_1\cdot{\frac{1-q^n}{1-q}}\) dla \(q\neq 1\) \(S_n=a_1\cdot n\), dla \(q=1\) |
| szereg geometryczny | \(a_1+a_1\cdot{q}+a_1\cdot{q^2}+a_1\cdot{q^3}+...+a_1\cdot{q^{n-1}}+...\) |
| suma szeregu geometrycznego | \(S=\frac{a_1}{1-q}\) |
Pytania
Co to jest ciąg liczbowy Fibonacciego?
Ciąg Fibonacciego jest jednym z przykładów ciągów liczbowych, określonych w taki sposób, że pierwszy jego wyraz jest zerem, drugi jednością, a każdy następny jest sumą dwóch poprzednich. Oto kilkanaście pierwszych wyrazów ciągu Fibonacciego: \(0,1,1,2,3,5,8,13,21,34,55,89,144,233,...\)
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Napisać:
a) trzy początkowe wyrazy ciągu \(a_n=\frac{n[2-(-2)^{n+1}]}{n+1}\) oraz znaleźć dziewiąty wyraz tego ciągu.
b) pięć początkowych wyrazów ciągu \(\begin{cases}a_1=2 \\ a_2=4 \\ a_n=a_{n-2}+2a_{n-1}, \ dla \ n\geq 3 \end{cases}\)

Zadanie nr 2 — maturalne.
Ciąg \((b_n)\) jest określony wzorem \(b_n=3n^2-25n\) dla każdej liczby naturalnej \(n\geq 1\). Liczba niedodatnich wyrazów ciągu \((b_n)\) jest równa
A. 14
B. 13
C. 9
D. 8

Zadanie nr 3 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2n^2\) dla \(n\geq 1\). Różnica \(a_5-a_4\) jest równa
A. \(4\)
B. \(20\)
C. \(36\)
D. \(18\)

Zadanie nr 4 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{2n^2-30n}{n}\) dla każdej liczby naturalnej \(n\geq 1\). Wtedy \(a_7\) jest równy
A. (-196)
B. (-32)
C. (-26)
D. (-16)

Zadanie nr 5 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2^n\cdot (n+1)\) dla każdej liczby naturalnej \(n\geq 1\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wyraz \(a_4\) jest równy
A. 64
B. 40
C. 48
D. 80
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-08-20, A-293
Data aktualizacji artykułu: 2023-05-12


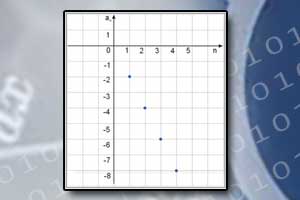 Wykres ciągu
Wykres ciągu Monotoniczność ciągu
Monotoniczność ciągu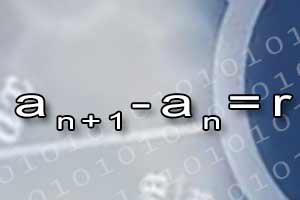 Ciąg arytmetyczny
Ciąg arytmetyczny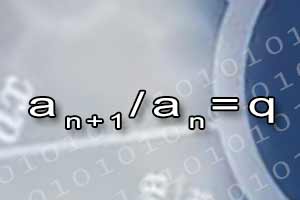 Ciąg geometryczny
Ciąg geometryczny