Długość wektora
Jak obliczyć długość wektora? Podamy dwa wzory, w przypadku gdy dane są współrzędne tego wektora (składowe wektora), a także w przypadku gdy mamy dane współrzędne początku i końca wektora.
Długość wektora \(\vec{a}\) (moduł wektora) będziemy oznaczać przez \(|\vec{a}|\) lub \(a\).
Aby obliczyć długość dowolnego wektora \(\vec{a}\), będziemy korzystać ze wzoru:
gdzie \(a_x\) i \(a_y\) oznaczają miary składowych wektora \(\vec{a}\).
Zastosujmy powyższy wzór na długość wektora w zadaniu:
Przykład
Oto jak liczymy długość wektora \(\vec{a}=[4,-3]\):
\(|\vec{a}|=\sqrt{4^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5\)
Gdy dane są jedynie współrzędne początku \(A=(x_A,y_A)\) i końca wektora \(B=(x_B,y_B)\), to moduł wektora \(\vec{AB}\) obliczymy ze wzoru:
Powyższy wzór wynika z własności współrzędnych wektora. Zauważ, że długość wektora obliczamy identycznie jak długość odcinka.
Przykład
Dany jest punkt \(A=(1,2)\) i \(B=(-2,3)\). Jaką długość ma wektor \(\vec{AB}\)?
Korzystamy z powyższego wzoru:
\(|\vec{AB}|=\sqrt{(-2-1)^2+(3-2)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Rozwiązanie zadania: Oblicz długość wektora:
a) \(\vec{a}=[-3,4]\)
b) \(\vec{b}=5\vec{i}-2\vec{j}\)
c) \(\vec{c}=-\vec{j}\)
d) \(\vec{0}\)
e) \(\vec{AB}, A=(2,3), B=(-2,-3)\)

Zadanie nr 2.
Dany jest punkt \(A=(-1,1)\). Znaleźć punkt \(B\), jeżeli wiadomo, że \(|\vec{AB}|=4\).

Zadanie nr 4.
Dany jest wektor \(\vec{a}=[3,4]\). Przez jaką liczbę należy go pomnożyć, aby jego długość była równa 1?
Inne zagadnienia z tej lekcji
© medianauka.pl, 2008-04-24, A-23
Data aktualizacji artykułu: 2023-07-10


 Wektor
Wektor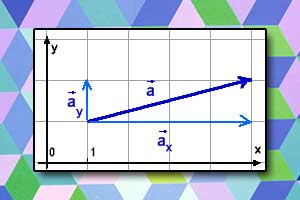 Współrzędne wektora
Współrzędne wektora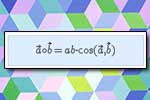 Iloczyn skalarny
Iloczyn skalarny Mnożenie wektora przez liczbę
Mnożenie wektora przez liczbę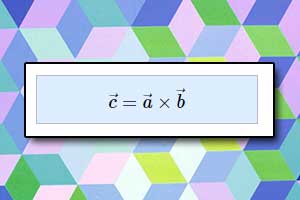 Iloczyn wektorowy
Iloczyn wektorowy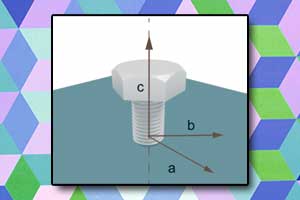 Reguła śruby prawoskrętnej
Reguła śruby prawoskrętnej