Funkcja potęgowa
Funkcja potęgowa o wykładniku rzeczywistym \(a\) jest to funkcja w postaci:
Przykłady
Przykłady funkcji potęgowych:
- \(y=x^2\)
- \(y=x^{-1}\), czyli \(y=\frac{1}{x}\)
- \(y=x^{\frac{1}{2}}\), czyli \(y=\sqrt{x}\)
- \(y=x^{\pi}\)
Dziedzina funkcji potęgowej
Dziedzina funkcji potęgowej jest uzależniona od wartości wykładnika.
| Wykładnik | Dziedzina funkcji potęgowej |
|---|---|
| \(a\in \mathbb{C}, a\geq 0\) | \(\mathbb{R}\) |
| \(a\in \mathbb{C}, a<0\) | \(\mathbb{R}\setminus{\lbrace}0\rbrace\) |
| \(a\in \mathbb{R}\setminus \mathbb{C}, a>0\) | \(\mathbb{R}_+\cup{\lbrace}{0}\rbrace\) |
| \(a\in \mathbb{R}\setminus \mathbb{C}, a<0\) | \(\mathbb{R}_+\) |
Własności funkcji potęgowej
Funkcja potęgowa jest parzysta dla wykładników naturalnych parzystych i nieparzysta dla wykładników naturalnych nieparzystych.
W dalszej części lekcji omawiamy wykres funkcji potęgowej.
Pytania
Czy funkcja kwadratowa jest funkcją potęgową?
Co do zasady funkcja kwadratowa nie jest funkcją potęgową. Jedynie szczególny przypadek funkcji kwadratowej można nazwać funkcją potęgową, a mianowicie jednomian \(f(x)=x^2\).
Czy funkcja wykładnicza jest funkcją potęgową?
Nie. Funkcja wykładnicza charakteryzuje się tym, że niewiadoma znajduje się w wykładniku potęgi, a w funkcji potęgowej niewiadoma znajduje się w podstawie potęgi. To dwie różne funkcje o różnych własnościach.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-10-10, A-353
Data aktualizacji artykułu: 2023-04-26


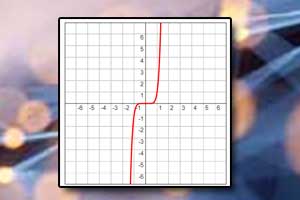 Wykres funkcji potęgowej
Wykres funkcji potęgowej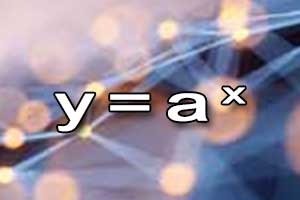 Funkcja wykładnicza
Funkcja wykładnicza