Funkcja różnowartościowa
Funkcję \(f(x)\) nazywamy różnowartościową w zbiorze \(A\), będącym podzbiorem dziedziny funkcji \(f(x)\), jeżeli dla każdych \(x_1,x_2\in A\) prawdziwa jest implikacja: \((x_1 \neq x_2) \Rightarrow f(x_1) \neq f(x_2)\).
Powyższa definicja oznacza, że funkcja różnowartościowa, to taka funkcja, która różnym argumentom przyporządkowuje różne wartości funkcji.
Przykłady
Przykłady funkcji różnowartościowych:
- \(y=2x+1\)
- \(y=\frac{1}{x}\)
- \( y=\log x\)
A oto przykłady funkcji, które funkcjami różnowartościowymi nie są:
- \(y=5\) (każdemu argumentowi przyporządkowana jest liczba 5)
- \(y=x^2\) (na przykład liczbom 2 i -2 przyporządkowana jest taka sama wartość 4)
- \(y=|x|\)
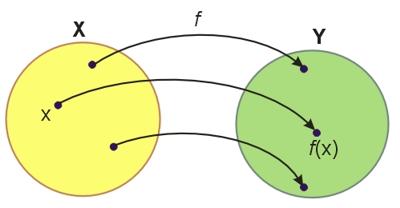
Poniższa ilustracja przedstawia przykład funkcji różnowartościowej.
Pytania
Jak wykazać różnowartościowość funkcji?
Zakładamy, że \(x_1\neq x_2\), czyli \(x_1-x_2\neq 0\). Musimy wykazać prawdziwość naszej tezy: \(f(x_1)\neq f(x)2\), czyli \(f(x_1)-f(x_2)\neq0\).
Dla przykładu zbadajmy funkcję liniową \(y=ax+b\). Mamy więc:
\(f(x_1)=ax_1+b\)
\( f(x_2)=ax_2+b\)
\(f(x_1)-f(x_2)=ax_1+b-(ax_2+b)=ax_1-ax_2=a(x_1-x_2)\)
Ponieważ założenie mówi, że \(x_1-x_2\neq 0\), czyli \(x_1-x_2\neq 0\), to mamy dwa przypadki:
a) gdy \(a=0, f(x_1)-f(x_2)=0\), czyli udowodniliśmy, że funkcja stała nie jest różnowartościowa,
b) gdy \(a\neq 0, f(x_1)-f(x_2)\neq 0\), czyli udowodniliśmy, że funkcja liniowa jest różnowartościowa w każdym innym przypadku.
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-05-18, A-209
Data aktualizacji artykułu: 2023-04-05

 Funkcja
Funkcja Monotoniczność funkcji
Monotoniczność funkcji Funkcja okresowa
Funkcja okresowa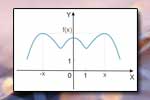 Parzystość funkcji
Parzystość funkcji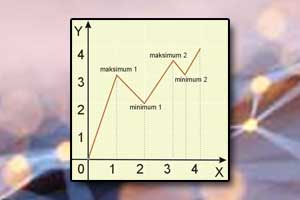 Ekstremum funkcji
Ekstremum funkcji Funkcja odwrotna i tożsamościowa
Funkcja odwrotna i tożsamościowa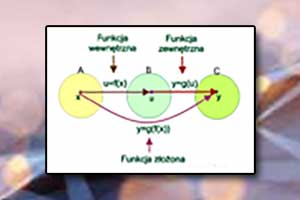 Funkcja złożona
Funkcja złożona