Pole wycinka kołowego
Pole wycinka kołowego o kącie środkowym ![]() (kąt wyrażony w stopniach) i promieniu r jest równe:
(kąt wyrażony w stopniach) i promieniu r jest równe:
Przykład
Obliczyć pole wycinka kołowego przedstawionego na rysunku o promieniu 2.
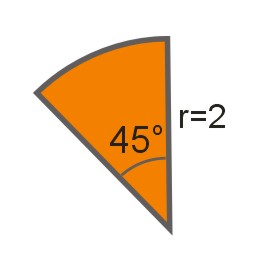
Kąt środkowy wycinka kołowego ma miarę 45° (zobacz rysunek). Zatem pole wycinka kołowego obliczamy następująco:
\(P=\frac{\alpha}{360}\cdot \pi r^2 = \frac{45}{360}\cdot \pi \cdot 2^2=\frac{1}{8}\cdot 4\pi=\frac{1}{2}\pi\)
Pole wycinka pierścienia kołowego
Pole wycinka pierścienia kołowego o kącie środkowym \(\alpha\) (kąt wyrażony w stopniach) i promieniu małym \(a\) i dużym \(b\) jest równe:
Przykład
Obliczyć pole wycinka pierścienia kołowego przedstawionego na rysunku o promieniu 2 i 1.
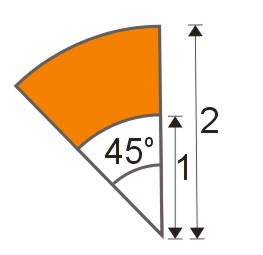
Kąt środkowy wycinka pierścienia kołowego ma miarę 45° (zobacz rysunek). Zatem pole wycinka pierścienia kołowego obliczamy następująco:
\(P=\frac{\alpha}{360}\cdot \pi (b^2-a^2) = \frac{45}{360}\cdot \pi \cdot (2^2-1^2)=\)
\( =\frac{1}{8}\cdot \pi \cdot (4-1)=\frac{1}{8}\pi\cdot 3=\frac{3}{8}\pi\)
Zadania z rozwiązaniami

Zadanie nr 1.
Jakie pole zakreśla na zegarze sekundnik w czasie 1 sekundy, jeżeli długość tej wskazówki jest równa 20 cm?

Zadanie nr 2.
Jaką część należy wyciąć z pierścienia kołowego, aby jego pole było równe \(\frac{\pi}{8}\)?

Zadanie nr 3 — maturalne.
Punkty \(A, B, P\) leżą na okręgu o środku \(S\) i promieniu 6. Czworokąt \(ASBP\) jest rombem, w którym kąt ostry \(PAS\) ma miarę 60° (zobacz rysunek).
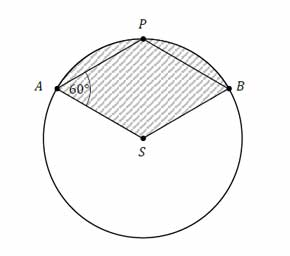
Pole zakreskowanej na rysunku figury jest równe
A. \(6\pi\)
B. \(9\pi\)
C. \(10\pi\)
D. \(12\pi\)
Inne zagadnienia z tej lekcji
© medianauka.pl, 2010-12-10, A-1048
Data aktualizacji artykułu: 2023-06-14

 Pierścień kołowy
Pierścień kołowy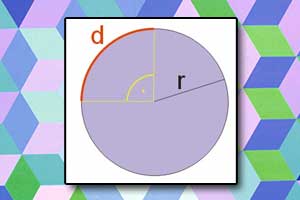 Łuk okręgu
Łuk okręgu Okrąg i koło
Okrąg i koło