Potęga o wykładniku niewymiernym
Sposób, w jaki obliczamy potęgę o wykładniku niewymiernym \(w\), określamy tylko dla podstawy a>0. Korzystamy tutaj z ciągu przybliżeń z niedomiarem oraz nadmiarem liczby \(w\). Tworzymy na tej podstawie ciąg potęg o wykładniku wymiernym. Kres dolny oraz kres górny zbioru wyrazów tych ciągów, to właśnie wartość potęgi o wykładniku niewymiernym.
Przykłady
Na przykładzie zobaczmy, w jaki sposób wyznaczamy potęgę \(2^{\pi}\).
Liczba \(\pi=3.1415926535...\)
Tworzymy ciąg z niedomiarem: \((3,1, 3,14, 3,141, 3,1415, ...)\) i ciąg z nadmiarem: \((3,2, 3,15, 3,142, 3,1416, ...)\) oraz odpowiadające im ciągi potęg:
\((2^{3,1},2^{3,14},2^{3,141},2^{3,1415},...)\)
\((2^{3,2},2^{3,15},2^{3,142},2^{3,1416},...)\)
Każdy z tych wyrazów ciągu jesteśmy w stanie policzyć, korzystając z wiedzy na temat potęgi o wykładniku wymiernym. Dla przykładu policzymy wartość pierwszego wyrazu pierwszego ciągu.
\(2^{3,1}=2^{3\frac{1}{10}}=2^{\frac{31}{10}}=\sqrt[10]{2^{31}}=8\sqrt[10]{2}\)
Jest to już pewne przybliżenie szukanej potęgi (zauważ, że także niewymierne). W zależności od wymaganej dokładności wyniku bierzemy pod uwagę kolejny wyraz jednego z powyższych ciągów.
Możemy napisać, że \(2^{\pi}\approx{8}\sqrt[10]{2}\).
Działania na potęgach o wykładniku niewymiernym
Jeżeli \(a>0\) i \(b>0\), to dowolnych liczb rzeczywistych \(m\) i \(n\) prawdziwe są wszystkie własności działań na potęgach.
Przykłady
- \(2^{\sqrt{3}}\cdot{2^{-\sqrt{3}}}=2^{\sqrt{3}-\sqrt{3}}=2^0=1\)
- \(2^{\pi}\cdot{7^{\pi}}=14^{\pi}\)
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-10-03, A-349
Data aktualizacji artykułu: 2023-03-12

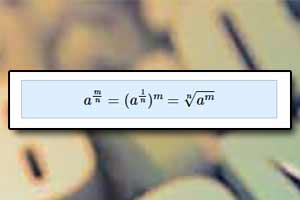 Potęga o wykładniku wymiernym
Potęga o wykładniku wymiernym Działania na potęgach
Działania na potęgach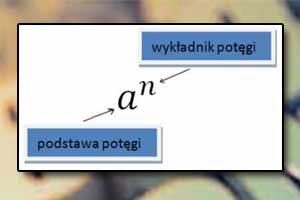 Potęgowanie
Potęgowanie