Aksjomaty planimetrii
Planimetria jest działem geometrii (słowo „geometria” pochodzi od słów greckich: ge — ziemia i metreo — mierzę), która zajmuje się własnościami płaszczyzny i jej podzbiorów. Planimetria jest więc geometrią płaszczyzny. Planimetria zbudowana na jednej płaszczyźnie stosuje się do każdej innej płaszczyzny. Planimetria bada własności figur geometrycznych płaskich.
Przestrzeń, punkt, prosta, płaszczyzna
Zbiór wszystkich punktów to przestrzeń. Oznaczamy ją grecką literą omega — \(\Omega\).
Punkt, prosta, płaszczyzna są pojęciami podstawowymi, których się nie definiuje, a ich własności wynikają z aksjomatów (pewników, twierdzeń podstawowych, których się nie dowodzi).
Figura płaska jest to dowolny zbiór punktów zawartych w płaszczyźnie.
Aksjomat o przynależności punktów do prostej
- Na każdej prostej leży nieskończenie wiele punktów.
- Przez każdy punkt przechodzi nieskończenie wiele prostych.
Pęk prostych
Pęk prostych jest to rodzina prostych przechodzących przez jeden punkt, nazywanym wierzchołkiem pęku.
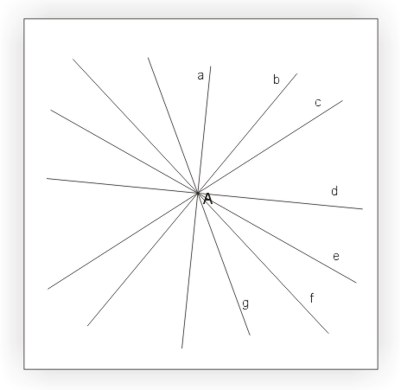
Ilustracja przedstawia pęk prostych \(a, b, c, d, e, f, g\) o wierzchołku \(A\).
Aksjomat o dwóch punktach i prostej
Przez dwa różne punkty przechodzi jedna i tylko jedna prosta.
Prostą wyznaczoną przez punkty \(A\) i \(B\) oznaczamy przez \(AB\). Z powyższych dwóch aksjomatów wynika wzajemne położenie prostych. Możliwe są tutaj trzy przypadki: dwie proste nie mają punktu wspólnego, mają jeden punkt wspólny lub są identyczne (mają nieskończenie wiele punktów wspólnych).
Proste równoległe, przecinające się i pokrywające się — definicja
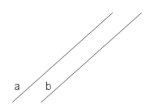
Proste \(a\) i \(b\) są równoległe, jeżeli nie mają punktu wspólnego. Używamy wówczas zapisu: \(a||b\).
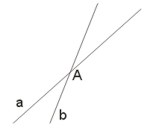
Proste \(a\) i \(b\) przecinają się, jeżeli mają jeden punkt wspólny. Możemy to zapisać następująco: \(a\cap b=\lbrace A\rbrace\) (częścią wspólną prostej \(a\) i \(b\) jest punkt \(A\)).
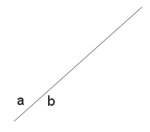
Proste \(a\) i \(b\) pokrywają się, jeżeli są identyczne, czyli \(a=b\). Proste te mają nieskończenie wiele punktów wspólnych. Możemy też powiedzieć, że prosta jest równoległa sama do siebie.
Aksjomat Euklidesa
Przez każdy punkt przechodzi dokładnie jedna prosta równoległa do danej prostej.

Animacja
Poniższa animacja jest ilustracją aksjomatu Euklidesa.
Kierunek prostej
Kierunek prostej jest to rodzina wszystkich prostych równoległych do danej prostej.
Uporządkowanie punktów na prostej
Aksjomat — porządkowanie punktów na prostej
Na prostej istnieją dokładnie dwa uporządkowania takie, że dla dowolnych punktów \(A, B, C\), należącej do tej prostej zachodzą warunki:
- Jeżeli \(A\) poprzedza \(B\) przy jednym uporządkowaniu, to \(B\) poprzedza \(A\) przy drugim uporządkowaniu.
- Jeżeli \(B\) leży między \(A\) i \(C\), to \(|AB|+|BC|=|AC|\).
- Jeżeli \(|AB|+|BC|=|AC|\) i punkty \(A, B, C\) są różne, to \(B\) leży między \(A\) i \(C\).
Prosta ma dwa naturalne uporządkowana: jedno, w którym \(A\) poprzedza \(B\) i przeciwne do niego, w którym \(B\) poprzedza \(A\).
Zwrot prostej
Każde uporządkowanie prostej nazywamy zwrotem prostej.
Współliniowość punktów — prawo trójkąta
Definicja
Punkty są współliniowe (kolinearne), jeżeli należą do jednej prostej.
Warunek konieczny i wystarczający niewspółliniowowści
Punkty \(A, B, C\) nie są współliniowe wtedy i tylko wtedy, gdy \(||AB|-|BC||<|AC|<|AB|+|BC|\).
Warunek konieczny i wystarczający współliniowowści
Punkty \(A, B, C\) są współliniowe wtedy i tylko wtedy, gdy \(|AC|=|AB|+|BC|\) lub \(|AC|=||AB|-|BC||\).
Gdy połączymy oba powyższe twierdzenia, otrzymamy:
Prawo trójkąta
Dla dowolnych punktów \(A, B, C\) zawsze zachodzi nierówność:
Równość zachodzi w przypadku, gdy punkty są współliniowe.
Pytania
Gdzie znajdę wzory z planimetrii?
Aby znaleźć odpowiednie wzory z planimetrii, przejdź do naszego działu geometria i wybierz odpowiedni rodzaj figur płaskich (na przykład trójkąty, okrąg itp.)
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Ile różnych prostych wyznaczają cztery różne punkty na płaszczyźnie?

Zadanie nr 2.
Ile różnych prostych wyznacza n różnych punktów na płaszczyźnie, jeżeli żadne z trzech punktów nie są współliniowe?

Zadanie nr 3.
Sprawdzić, czy istnieją takie punkty \(A, B, C\), że
a) \(|AB|=10, |AC|=5, |BC|=5\)
b) \(|AB|=10, |AC|=4, |BC|=5\)
c) \(|AB|=10, |AC|=6, |BC|=5\)

Zadanie nr 4.
Sprawdzić, czy punkty \(A, B, C\) są współliniowe (kolinearne), jeżeli:
a) \(|AB|=7, |BC|=5,5 ,|AC|=1,5\)
b) \(|AB|=4+2\sqrt{3}, |BC|=2+\sqrt{3} ,|AC|=3\sqrt{3}\)

Zadanie nr 5.
Zbadać, czy z odcinków o długości 5,3 i 1 można zbudować trójkąt.

Zadanie nr 6.
Punkty \(A, B, C\) są współliniowe i \(|AB|=7, |BC|=6\). Jaką liczbą jest \(|AC|\)?

Zadanie nr 7.
Dane są odcinki o długościach \(|AB|=5, |BC|=8\). Jaką długość powinien mieć odcinek \(\overline{AC}\), aby można było zbudować trójkąt \(ABC\)?

Zadanie nr 8 — maturalne.
Z odcinków o długościach: \(5, 2a+1, a-1\) można zbudować trójkąt równoramienny. Wynika stąd, że
A. \(a=6\)
B. \(a=4\)
C. \(a=3\)
D. \(a=2\)
Inne zagadnienia z tej lekcji
© medianauka.pl, 2010-10-10, A-973
Data aktualizacji artykułu: 2023-05-21


 Odległość punktów
Odległość punktów Półprosta
Półprosta Odcinek
Odcinek Łamana
Łamana Wzajemne położenie prostych
Wzajemne położenie prostych