Równanie liniowe
Równanie liniowe z jedną niewiadomą jest to równanie w postaci:
gdzie \(a\) i \(b\) są liczbami rzeczywistymi, \(x\) — niewiadoma.
Przykłady
Oto przykłady równań liniowych z jedną niewiadomą:
- \(5x+1=0\) (\(a=5\) i \(b=1\));
- \(-x=0\) (\(a=-1\) i \(b=0\));
- \(\frac{x}{2}+\sqrt{7}=0\) (\(a=\frac{1}{2}\) i \(b=\sqrt{7}\));
- \(2x=5\) (\(a=2\) i \(b=-5\));
- \(-6-x=0\) (\(a=-1\) i \(b=-6\));
- \((\frac{1}{7}-\sqrt{5})x-1+\sqrt{3}=0\).
Równanie pierwszego stopnia jest to równanie liniowe w przypadku, gdy \(a\neq{0}\).
Nazwa pochodzi od potęgi, w jakiej znajduje się niewiadoma — tutaj jest to pierwsza potęga.
Rozwiązanie równania liniowego
Rozwiążmy równanie pierwszego stopnia:
\(ax+b=0\)
\(ax=-b/:a\)
\(x=-\frac{b}{a}\)
Zatem równanie pierwszego stopnia ma jeden pierwiastek równy:
Pierwiastek równania pierwszego stopnia jest punktem zerowym funkcji liniowej.
Przykłady
Rozwiązać równanie \(2x-4=0\)>.
Rozwiązanie:
\(2x-4=0\)
\(2x=4/:2\)
\(x=2\)
Zgodnie z interpretacją geometryczną pierwiastka równania wykres funkcji \(y=2x-4\), powinien przecinać oś \(OX\) w punkcie \(x_0=2\). Ilustruje to poniższy rysunek.
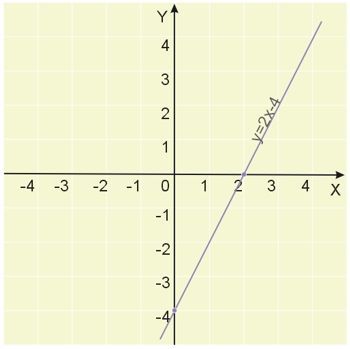
W przypadku równania liniowego, w którym zarówno \(a\), jak i \(b\) jest równe zeru, to otrzymujemy równanie tożsamościowe \(0=0\) (każda liczba spełnia równanie \(0\cdot x+0=0\)), a przypadek ten ilustruje prosta leżąca na osi \(OX\).
W przypadku równania liniowego, w którym \(a=0\), natomiast \(b\) jest różne od zera, to otrzymujemy równanie sprzeczne (żadna liczba nie spełnia równania \(0\cdot{x+b=0}\)), a przypadek ten ilustruje prosta równoległa do osi \(OX\) przecinająca oś \(OY\) w punkcie \(y_0=b\).
Rozwiązywanie równań liniowych
Oto prosty przykład rozwiązania równania liniowego:
Zadanie
Rozwiązać równanie: \(-\frac{1}{2}x-\frac{1}{3}=0\).
Rozwiązanie:
\(-\frac{1}{2}x-\frac{1}{3}=0\)
\(-\frac{1}{2}x=\frac{1}{3}/\cdot{(-2)}\)
\(x=-\frac{2}{3}\)
Odpowiedź: \(x=-\frac{2}{3}\).
Równanie liniowe z parametrem
Nie zawsze w równaniu liniowym jawnie zapisywane są liczby. Zamiast nich stosuje się oznaczenia literowe, nazywane parametrami. Równanie zawierające takie oznaczenia literowe nazywamy równaniem z parametrem. Zawsze w takim równaniu musimy wskazać niewiadomą lub ze względu na jaką zmienną należy rozwiązać dane równanie.
Po co parametryzować równania? W celu uogólnienia równania i jego rozwiązania. Zamiast rozwiązywać osobno równania: \(x+1=0, x+2=0, x+443,225=0\) można rozwiązać równanie \(x+m=0\), otrzymać wynik \(x=-m\) i w ten oto sposób rozwiązać nie tylko wymienione tutaj równania, ale wszystkie inne równania w tej postaci za jednym razem!
Przykłady
Równanie \(mx-2x=1\) jest przykładem równania z parametrem, o ile jest informacja, że \(x\) lub \(m\) jest niewiadomą. Równanie to można rozwiązać ze względu na \(x\), wówczas \(m\) traktujemy jak liczbę rzeczywistą, możemy też rozwiązać to równanie ze względu na \(m\), a \(x\) traktować jako parametr.
1) Rozwiążemy to równanie ze względu na \(x\).
\(mx-2x=1\)
\(x(m-2)=1\)
Teraz mogą wystąpić różne przypadki.
Jeżeli \(m-2\neq{0}\Leftrightarrow{m\neq{2}}\), możemy dokonać przekształcenia:
\(x(m-2)=1/:(m-2)\)
\(x=\frac{1}{m-2}\)
Jeżeli \(m-2=0\Leftrightarrow{m=2}\), mamy do czynienia z równaniem sprzecznym:
\(x\cdot{0=1}\)
\(0=1\)
Równanie ma jedno rozwiązanie \(x_0=\frac{1}{m-2}\) dla \(m\neq{2}\) oraz nie ma rozwiązań w przypadku, gdy \(m=2\).
2) Rozwiążemy to równanie ze względu na \(m\). Zatem \(x\) traktujemy jak zwykłą liczbę.
\(mx-2x=1\)
\(mx=1+2x\)
Dla \(x\) różnego od zera mamy jedno rozwiązanie \(m_0=\frac{1+2x}{x}\), natomiast dla \(x=0\) równanie nie ma rozwiązania (jest sprzeczne).
Czasem równanie wygląda groźnie ze względu na parametry, których może być wiele w równaniu, jednak jeżeli tylko mamy do czynienia z równaniem liniowym, rozwiązanie takiego równania nie powinno być trudne.
Przykład
Przykład takiego równania z parametrami \(a\) i \(b\) jest w rzeczywistości łatwy do rozwiązania:
\(\sqrt{a^2+1}+\frac{x}{2}-b^4=\log_2{a-b}\)
\({\frac{1}{2}x=\log_2{a-b}-\sqrt{a^2+1}+b^4/\cdot{2}}\)
\({x=2\log_2{a-b}-2\sqrt{a^2+1}+2b^4}\)
Zadania z treścią
Osobną grupę zadań stanowią zadania z treścią. Najważniejsze w procesie rozwiązywania takich zadań jest dobre oznaczenie niewiadomej i zapisanie zdania logicznego wypowiadanego w treści zadania za pomocą równania. Poniżej kilka przykładów.
Przykład 1
Jeśli dodamy do siebie wiek Janka, który jest o rok starszy od Krzysia do wieku Krzysia, to otrzymamy liczbę 15. W jakim wieku są chłopcy?
Oznaczamy i opisujemy niewiadome:
\(x\) — wiek Janka,
\(x-1\) — wiek Krzysia (Krzyś jest młodszy o rok).
Zapisujemy wypowiedziane w treści zdanie logiczne (suma lat chłopców jest równa 15).
\(x+(x-1)=15\)
\(2x-1=15\)
\(2x=16/:2\)
\(x=8\)
\(x-1=7\)
Odpowiedź: Janek ma 8 lat, a Krzyś 7.
Przykład 2
Jaką kwotę musi Janek przelać na lokatę o oprocentowaniu 5% w skali roku, aby po roku stać go było na zakup roweru, który kosztuje 1200 zł?
\(x\) - kwota kapitału.
Układamy równanie: kwota kapitału i kwota odsetek po roku musi być równa 1200 zł.
\(x+x\cdot 5\%=1200\)
\(x+\frac{5}{100}x=1200\)
\(\frac{105}{100}x=1200/\cdot{\frac{100}{105}}\)
\(x=\frac{120000}{105}\)
\(x\approx{1142,86}\)
Odpowiedź: Aby Janek mógł kupić rower za 1200 zł, musi włożyć na roczną lokatę o oprocentowaniu 5% kwotę 1142,86 zł.
Kalkulator

Kalkulator równań liniowych
Wpisz równanie liniowe
y= x+
Pytania
Ile rozwiązań może mieć równanie pierwszego stopnia z jedną niewiadomą?
Równanie takie może mieć jedno rozwiązanie, zero rozwiązań, gdy jest to równanie sprzeczne (np. \(x-1=x+1\)) lub nieskończenie wiele rozwiązań, w przypadku, gdy jest to tożsamościowe (np. \(x+1=2x+2\)).
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Rozwiązać równanie:
a) \(5x-3=7x+8\)
b) \(\sqrt{2}x+1=x+\sqrt{2}\)
c) \(\frac{1}{2}x-\frac{3}{7}=\frac{x}{2}-2\)

Zadanie nr 4.
Dla jakiej wartości parametru \(m\) rozwiązaniem równania \(x-m+1=3x-2\) jest liczba 2?

Zadanie nr 5.
Rozwiązać równanie \(\frac{x}{m-2}+m=5\) ze względu na zmienną x.

Zadanie nr 6.
Jacek jest o 3 lata starszy od Maćka. Razem chłopcy mają 15 lat. Ile lat ma każdy z chłopców?

Zadanie nr 7.
Na jaki procent należy włożyć na lokatę 200 zł, aby po roku oszczędzania otrzymać 5 zł odsetek?

Zadanie nr 8.
Rybak złowił szczupaka. Na pytanie, jak wielka jest ryba, odpowiedział zagadkowo: "Łeb szczupaka mierzy 6 cm, tułów ma długość taką jak głowa i ogon razem, przy czym trzy czwarte ogona mierzą tyle ile głowa i ćwierć długości głowy". Jaką długość ma szczupak?
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-06-24, A-245
Data aktualizacji artykułu: 2023-05-02


 Równania z wartością bezwzględną
Równania z wartością bezwzględną Regresja liniowa
Regresja liniowa