Twierdzenie Pitagorasa
Rozważamy dowolny trójkąt prostokątny.
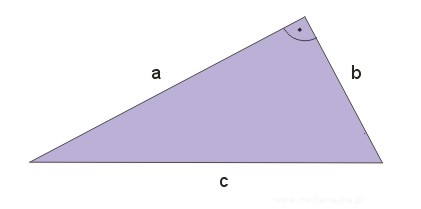
Powyższy wzór wyraża właśnie słynne twierdzenie Pitagorasa.
Interpretacja twierdzenia Pitagorasa
Twierdzenie Pitagorasa można rozumieć jako związek między dowolnymi liczbami, które stanowią długość boków w trójkącie prostokątnym. Można jednak to twierdzenie rozumieć tak, że pole kwadratu, którego bokiem jest przeciwprostokątna, jest równe polu kwadratów, których bokami są przyprostokątne (zobacz poniższy rysunek).
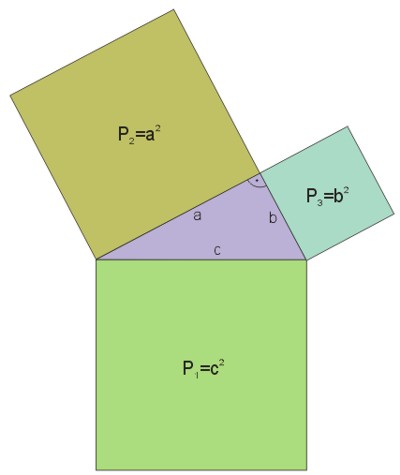
Zastosowanie twierdzenia Pitagorasa
Twierdzenie Pitagorasa jest bardzo często wykorzystywanym twierdzeniem w matematyce. Ma bardzo wiele zastosowań. Poniżej przykład jego wykorzystania.
Przykład
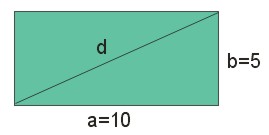
Dany jest prostokąt o bokach 5 i 10. Obliczyć długość przekątnej tego prostokąta.
Sporządzamy rysunek. Przekątna o długości \(d\) dzieli prostokąt na dwa trójkąty prostokątne. Korzystamy więc z twierdzenia Pitagorasa:
\(d^2=10^2+5^2\)
\(d^2=125\)
\(d=\sqrt{125}=5\sqrt{5}\)
Twierdzenie odwrotne do twierdzenia Pitagorasa
Jeżeli w pewnym trójkącie suma kwadratów długości dwóch jego boków jest równa kwadratowi długości trzeciego boku, to trójkąt ten jest trójkątem prostokątnym.
Ciekawostki
Co ciekawe, prawdziwe jest także następujące twierdzenie:
Suma pól podobnych figur płaskich zbudowanych na przyprostokątnych trójkąta prostokątnego jest równa polu figury podobnej do poprzednich, zbudowanej na przeciwprostokątnej tego trójkąta.
Trójka pitagorejska
W matematyce pewne liczby naturalne, które spełniają twierdzenie Pitagorasa, nazywamy pitagorejską trójką. Są to na przykład liczby: 3,4,5 lub 5,12,13. Jeśli długości boków trójkąta prostokątnego są pitagorejską trójką, to taki trójkąt nazywamy trójkątem pitagorejskim.
Pitagoras

Pitagoras © kengmerry — stock.adobe.com
Pitagoras był greckim matematykiem i filozofem, który żył w latach około 572-497 p.n.e. Uważany jest za twórcę początku teorii liczb.
Był twórcą pitagoreizmu, nurtu w filozofii, który uznawał za cel filozofii doskonalenie człowieka przez samoopanowanie i wiedzę. Do osiągnięć pitagorejczyków zaliczamy:
- Stworzenie podstaw teorii liczb, w tym odkrycie wielu ich własności.
- Podział liczb na parzyste i nieparzyste.
- Odkrycie liczb niewymiernych.
Szkoła Pitagorejska działała w Krotonie na południu Italii. Znakiem pitagorejczyków był pentagram.
Pitagoras nie jest autorem tego słynnego twierdzenia, ale jako pierwszy podał jego dowód. Twierdzenie to było znane już wcześniej!
Dowody twierdzenia Pitagorasa
Istnieje wiele dowodów twierdzenia Pitagorasa. Najczęściej spotykane to geometryczne dowody w postaci tak zwanej "układanki". Oto przykład takiego dowodu.
Dowód z Chou Pei Suan Ching

Pytania
Jak brzmi twierdzenie Pitagorasa?
W trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów przyprostokątnych.
Twierdzenie to można także sformułować inaczej. Na przykład tak:
Pole kwadratu zbudowanego na przeciwprostokątnej trójkąta prostokątnego jest równe sumie pól kwadratów zbudowanych na obu przyprostokątnych.
Co to jest wzór Pitagorasa?
To nic innego jak \(a^2+b^2=c^2\).
Co to jest trójkąt pitagorejski?
Trójkąt pitagorejski lub trójkąt Pitagorasa jest to trójkąt, którego boki są wyrażone liczbami naturalnymi \(a, b, c\) związanymi warunkiem \(a^2+b^2=c^2\). Są to trójkąty prostokątne.
Co to jest trójkąt egipski?
Trójkąt egipski jest szczególnym przypadkiem trójkąta pitagorejskiego. Jego boki mają długości odpowiednio 3, 4 i 5. Za pomocą listew odpowiedniej długości (3, 4, 5) w starożytnym Egipcie i w Babilonii wyznaczano kąty proste. To jednocześnie jedyny trójkąt pitagorejski, którego długości boków są kolejnymi liczbami naturalnymi.
Zadania z rozwiązaniami

Zadanie nr 1.
Oblicz wysokość w trójkącie równoramiennym o ramionach długości 10 i o podstawie długości 12.

Zadanie nr 2.
W trójkącie równoramiennym o ramionach długości 5 wysokość ma długość 4. Oblicz długość podstawy.

Zadanie nr 3.
W trójkącie prostokątnym miary dwóch kątów wewnętrznych są równe, a długość przeciwprostokątnej jest równa 6. Oblicz miarę kątów w tym trójkącie oraz długość boków.

Zadanie nr 4.
W trójkącie prostokątnym długości przyprostokątnych wynoszą odpowiednio 5 i 8. Oblicz długość przeciwprostokątnej.

Zadanie nr 5.
Znaleźć dowolny trójkąt prostokątny, dla którego kwadrat krótszej przyprostokątnej jest równy 1/4 kwadratu przeciwprostokątnej.

Zadanie nr 6.
Dane są kwadraty o polach \(\frac{1}{4}\) oraz \(\frac{1}{9}\). Jakie pole ma trzeci kwadrat, jeżeli wiadomo, że z ich boków można skonstruować trójkąt prostokątny?

Zadanie nr 7 — maturalne.
W trójkącie \(ABC\) bok \(BC\) ma długość 13, a wysokość \(CD\) tego trójkąta dzieli bok \(AB\) na odcinki o długościach \(|AD|=3\) i \(|BD|=12\) (zobacz rysunek obok). Długość boku \(AC\) jest równa
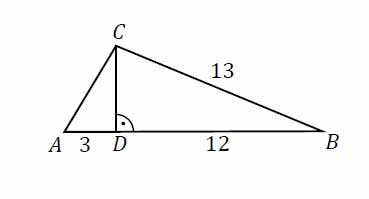
A. \(\sqrt{34}\)
B. \(\frac{13}{4}\)
C. \(2\sqrt{14}\)
D. \(3\sqrt{45}\)

Zadanie nr 8.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).

Zadanie nr 9.
Oblicz pole powierzchni i obwód trójkąta równobocznego o wysokości \(h=2 cm\).

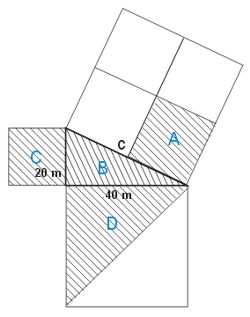
Zadanie nr 10.
Ceny poszczególnych działek są następujące:
A. 60 000 PLN
B. 50 000 PLN
C. 50 000 PLN
D. 100 000 PLN
Zakup której działki jest najbardziej opłacalny?

Inne zagadnienia z tej lekcji
© medianauka.pl, 2010-12-04, A-1042
Data aktualizacji artykułu: 2023-06-17

 Twierdzenia o trójkącie
Twierdzenia o trójkącie Twierdzenie sinusów, cosinusów i tangensów
Twierdzenie sinusów, cosinusów i tangensów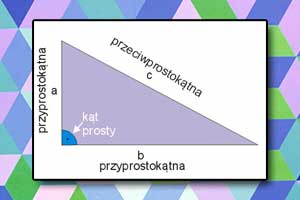 Trójkąt prostokątny
Trójkąt prostokątny Pole trójkąta i obwód trójkąta
Pole trójkąta i obwód trójkąta