Twierdzenie Talesa
Twierdzenie Talesa to jedno z najwcześniejszych i najważniejszych twierdzeń geometrii płaszczyzny. Powstało około V w. p.n.e.
Twierdzenie Talesa
Jeżeli dwie proste \(a_1\) i \(a_2\) przecinające się w punkcie \(O\) zostaną przecięte dwiema prostymi \(k\) i \(l\), które nie przechodzą przez punkt \(O\) i są równoległe, to odcinki wyznaczone przez punkt \(O\) i proste \(k\) i \(l\) na prostej \(a_1\) są proporcjonalne do odpowiednich odcinków wyznaczonych przez punkt \(O\) i proste \(k\) i \(l\) na prostej \(a_2\).
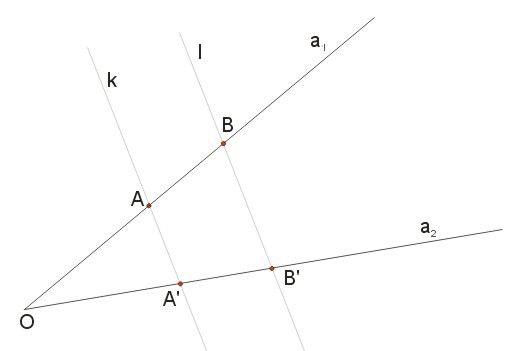
Proporcje wynikające z twierdzenia Talesa
Z twierdzenia Talesa wynikają następujące proporcje:
- \(\frac{|OA|}{|AB|}=\frac{|OA'|}{|A'B'|}\)
- \(\frac{|OA|}{|OA'|}=\frac{|AB|}{|A'B'|}\)
- \(\frac{|OA|}{|OB|}=\frac{|OA'|}{|OB'|}\)
- \(\frac{|AB|}{|OB|}=\frac{|A'B'|}{|OB'|}\)
Twierdzenie odwrotne do twierdzenia Talesa
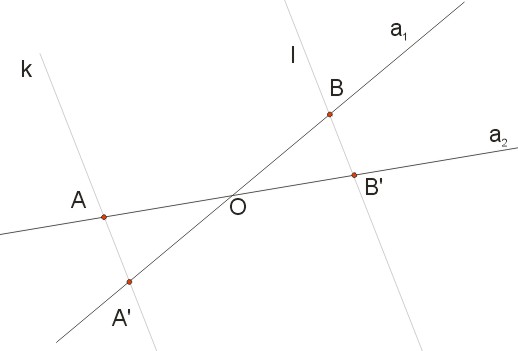
Jeżeli dwie proste \(a_1\) i \(a_2\) przecinające się w punkcie \(O\) zostaną przecięte dwiema prostymi \(k\) i \(l\), które nie przechodzą przez punkt \(O\) i odcinki wyznaczone przez punkt \(O\) i proste \(k\) i \(l\) na prostej \(a_1\) są proporcjonalne do odpowiednich odcinków wyznaczonych przez punkt \(O\) i proste \(k\) i \(l\) na prostej \(a_2\) i jeśli punkt \(O\) leży na obu odcinkach \(\overline{AB}, \ \overline{A'B'}\) albo nie leży na żadnym z nich, to proste \(k\) i \(l\) są równoległe.
Rozszerzone twierdzenie Talesa
Rzutując punkty podziału odcinków \(\overline{OA}, \overline{OB}\) w kierunku prostej \(a_2\), zauważamy, że z równoległości prostych \(k\), \(l\) wynika proporcja: \(|OA|:|OB|=|AA'|:|BB'|\).
Wnioski z twierdzenia Talesa
Twierdzenie 1
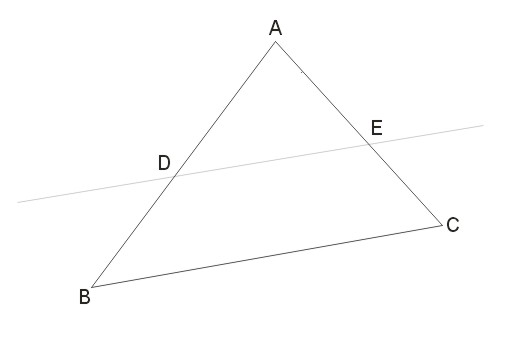
Prosta równoległa do jednego boku trójkąta i przecinająca pozostałe boki tego trójkąta odcina z tego trójkąta trójkąt o bokach proporcjonalnych do boków danego trójkąta.
\(\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}\)
Twierdzenie 2
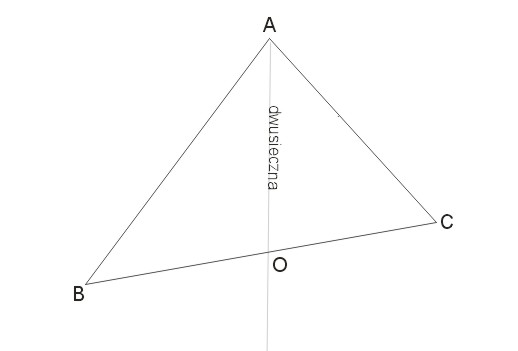
W trójkącie dwusieczna kąta wewnętrznego dzieli bok przeciwległy na odcinki proporcjonalne do boków przyległych.
\(\frac{OB}{OC}=\frac{AB}{AC}\)
Tales z Miletu

© Archivist — stock.adobe.com
Twierdzenie tutaj prezentowane sformułował prawdopodobnie Tales z Miletu, który żył w latach około 620-540 p.n.e. Tales był greckim filozofem, astronomem i matematykiem, twórcą jońskiej filozofii przyrody, w której woda była uważana za prapierwiastek rzeczywistości.
Niektórzy historycy wątpią co do tego, czy istniał w rzeczywistości i był autorem wszystkich głoszonych idei, czy też temu imieniu przyporządkowano osiągnięcia całej grupy uczonych starożytnej Grecji.
Zastosowania twierdzenia Talesa
Twierdzenie Talesa wykorzystywano już w starożytności do rozwiązania konkretnych problemów praktycznych, w tym obliczania odległości statków od brzegu i wysokości dużych obiektów.
Jak zmierzyć wysokość piramidy?
W prosty sposób można zmierzyć wysokości piramidy egipskiej na podstawie jej cienia. Metoda przedstawiona w przykładzie może być stosowana do mierzenia wysokości dowolnych obiektów, w tym: budynków, drzew itp.
Cień wbitej pionowo tyczki o znanej wysokości i piramidy powinny się pokrywać. Mierząc długość cieni, poznamy wysokość piramidy.
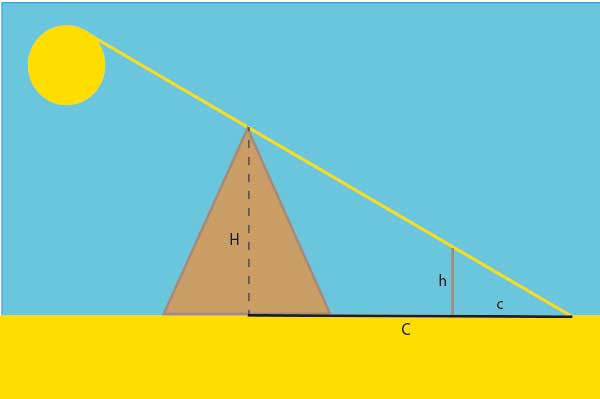
Na podstawie wniosku z twierdzenia Talesa (nie samego twierdzenia) można zapisać, że:
\(\frac{H}{C}=\frac{h}{c}\)
\(H=h\frac{C}{c}\)
Podział odcinka
Korzystając z twierdzenia Talesa, możemy dokonać proporcjonalnego podziału odcinka, co zostało omówione w odrębnym artykule.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1.
Podstawy trapezu mają długości 5 i 9, a ramiona 5 i \(\sqrt{41}\). Obliczyć obwód trójkąta utworzonego z podstawy trapezu i przedłużenia ramion tego trapezu.

Zadanie nr 2.
Prosta równoległa do boku \(AB\) trójkąta \(ABC\) przecina bok \(AC\) w punkcie \(D\) oraz bok \(BC\) w punkcie \(E\). Obliczyć:
a) \(|AC|\), jeżeli \(|CD|=32, |CE|=24,|BC|=48\)>
b) \(|CD|\), jeżeli \(|CE|=6, |BE|=10, |AC|=24\)

Zadanie nr 3.
Odcinek o długości \(a\) podzielić na dwa odcinki w stosunku \(\frac{3}{5}\).

Zadanie nr 4.
Dane są odcinki o długościach: \(a, b, c\). Opisać sposób konstrukcji odcinka \(d\) o długości:
a) \(d=\frac{ab}{c}\)
b) \(d=\frac{b^2}{a}\)

Zadanie nr 5 — maturalne.
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|=6\), a punkt \(D\) jest środkiem podstawy \(AB\). Okrąg o środku \(D\) jest styczny do prostej \(AC\) w punkcie \(M\). Punkt \(K\) leży na boku \(AC\), punkt \(L\) leży na boku \(BC\), odcinek \(KL\) jest styczny do rozważanego okręgu oraz \(|KC|=|LC|=2\) (zobacz rysunek).
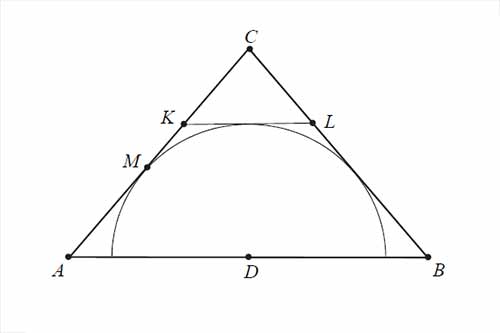
Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
Inne zagadnienia z tej lekcji
© medianauka.pl, 2010-12-04, A-1038
Data aktualizacji artykułu: 2023-06-09


 Podział odcinka
Podział odcinka Twierdzenie Pitagorasa
Twierdzenie Pitagorasa