Zadanie - określanie dziedziny funkcji logarytmicznej
Treść zadania:
Wyznaczyć dziedzinę funkcji \(y=\log_{(-x^2+2x)}{(x^3-x^2)}\).
 Rozwiązanie zadania
Rozwiązanie zadania
Musimy tutaj wziąć pod uwagę aż trzy warunki.
1) Po pierwsze liczba logarytmowana musi być większa od zera. Mamy więc warunek:
\(x^3-x^2>0\)
\(x^2(x-1)>0\)
Wyjęliśmy tutaj \(x^2\) przed nawias, doprowadzając wielomian do postaci iloczynowej. Otrzymaliśmy nierówność algebraiczną. Wielomian posiada dwa pierwiastki: \(0\) i \(1\). Sporządzamy siatkę znaków. Miejsca zerowe wyznaczają przedziały, które zapisujemy w kolumnach. W rzędach zapisujemy czynniki wielomianu. Ostatni wiersz, to znaki wielomianu. W kratkach zapisujemy znaki czynników dla wartości z poszczególnych przedziałów. Oto tabela:
| \(x\) | \((-\infty;0)\) | 0 | \((0;1)\) | 1 | \((1;+\infty)\) |
| \(x^2\) | + | 0 | + | + | + |
| \(x-1\) | - | - | - | 0 | + |
| \(x^2(x-1)\) | - | 0 | - | 0 | + |
Jak sprawdzić znak czynnika dla danego przedziału? Wystarczy dowolną liczbę z danego przedziału podstawić za niewiadomą i obliczyć wynik. Znak wyniku wpisujemy do kratki tabeli. (np. dla pierwszej kratki znak ustalamy w następujący sposób: weźmy dowolną liczbę z przedziału \((-\infty;0)\), niech to będzie \(-1\) i podstawmy do czynnika wielomianu \(x^2\) i otrzymujemy wynik \((-1)^2=1\), a więc dodatni. Znak "+" wpisujemy do odpowiedniej kratki) Jak znaleźć znak wielomianu? Wystarczy pomnożyć przez siebie w kolumnie jedności ze znakami z poszczególnych kratek. (np. dla pierwszej kolumny \(1\cdot (-1)=-1\), więc znak "-" wpisujemy w ostatnią kratkę pierwszej kolumny) Bezpośrednio z tabeli odczytujemy rozwiązanie. Interesują nas te przedziały, dla których wielomian \(x^2(x-1)\) jest dodatni, a więc:
\(x\in (1;\infty)\)
2) Warunek drugi wynika z tego, iż podstawa logarytmu musi być różna od jedności.
\(-x^2+2x\neq 1\)
\(-x^2+2x-1\neq 0/\cdot (-1)\)
\(x^2-2x+1\neq 0\)
\((x-1)^2\neq 0\)
\(x\neq 1\)
We fragmencie obliczeń zaznaczonym na żółto wykorzystujemy wzór skróconego mnożenia:
Doprowadzamy trójmian kwadratowy do postaci iloczynowej i stąd bezpośrednio odczytujemy wartość pierwiastka, równego jedności.
3) Warunek trzeci wynika z tego, że podstawa logarytmu musi być liczbą większą od zera. Mamy więc:
\(-x^2+2x>0\cdot (-1)\)
\(x^2-2x<0\)
\(x(x-2)<0\)
Mamy nierówność kwadratową i trójmian w postaci iloczynowej. Pierwiastki tego trójmianu, to liczby \(0\) i \(2\). Rozwiązanie odczytujemy ze szkicu wykresu. Współczynnik \(a\) jest dodatni, więc ramiona paraboli skierowane są do góry i wykres przecina oś \(OX\) w punktach \(0\) i \(2\). Szukamy wartości funkcji mniejszych od zera.
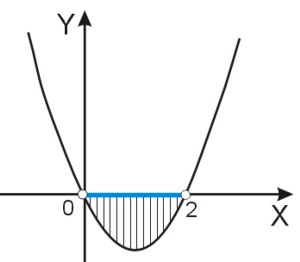
\(x\in(0;2)\)
Aby określić dziedzinę naszej funkcji, musimy uwzględnić jednocześnie wszystkie trzy warunki. Możemy je zapisać, używając do tego celu klamry:
\(\begin{cases}x\in (1;\infty)\\x\neq 1\\x\in(0;2) \end{cases}\)
\(\begin{cases}x^3-x^2>0\\-x^2+2x\neq 1\\-x^2+2x>0 \end{cases}\)
Dziedziną naszej funkcji będzie część wspólna powyższych zbiorów. Zaznaczmy je na osi liczbowej.
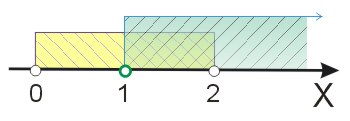
Rozwiązanie odczytujemy na podstawie powyższego rysunku:
\(x\in (1;2)\)
 Odpowiedź
Odpowiedź
© medianauka.pl, 2009-12-08, ZAD-417


Zadania podobne
Zadanie nr 2.
Wyznaczyć dziedzinę funkcji \(y=\log_{\frac{1}{2}}{\frac{x}{x+2}}\).
Zadanie nr 3.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{3}}{(x-3)}+1\).
Zadanie nr 5.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\).

