Zadanie - nierówność logarytmiczna
Treść zadania:
Rozwiązać nierówność logarytmiczną \(\log_{3}{x}+\log_{9}{x}\leq \log_{\frac{1}{3}}{\sqrt{5}}\).
Rozwiązanie zadania
Określamy dziedzinę danej nierówności, czyli zbiór wszystkich wartości \(x\), dla których nierówność (w tym logarytm) ma sens matematyczny.
Zgodnie z definicją logarytmu, wartość logarytmowana (w naszej nierówności jest to zmienna \(x\)) musi być większa od zera.
\(x\in (0;+\infty)\)
Rozwiązań nierówności logarytmicznej będziemy szukać tylko w zbiorze określonym powyżej.
W pierwszej kolejności musimy doprowadzić wszystkie logarytmy do takiej postaci, aby miały jednakową podstawę. Skorzystamy przy tym ze wzoru:
Zgodnie z powyższym mamy:
\(\log_{3}{x}+\log_{9}{x}\leq \log_{\frac{1}{3}}{\sqrt{5}}\)
\(\log_{3}{x}+\log_{9}{3}\cdot \log_{3}{x}\leq \log_{\frac{1}{3}}{3}\cdot \log_{3}{\sqrt{5}}\)
\(\log_{3}{x}+\frac{1}{2}\cdot \log_{3}{x}\leq -1\cdot \log_{3}{\sqrt{5}}/\cdot 2\)
\( 2\log_{3}{x}+\log_{3}{x}\leq -2\cdot \log_{3}{\sqrt{5}}\)
Dla wyjaśnienia: \(\log_{9}{3}=\frac{1}{2}\), bo \(9^{\frac{1}{2}}=\sqrt{9}=3\), \(\log_{\frac{1}{3}}{3}=-1\), bo \((\frac{1}{2})^{-1}=3\)
W dalszej części skorzystamy ze wzoru:
\(2\log_{3}{x}+\log_{3}{x}\leq -2\cdot \log_{3}{\sqrt{5}}\)
\(3\log_{3}{x}\leq -2\cdot \log_{3}{\sqrt{5}}\)
\(\log_{3}{x^3}\leq \log_{3}{(\sqrt{5})^{-2}}\)
\(\log_{3}{x^3}\leq \log_{3}{\frac{1}{5}}\)
Ponieważ podstawa logarytmu \(3>1\), to funkcja logarytmiczna jest rosnąca i nierówności argumentów odpowiada nierówność wartości funkcji. Możemy więc zapisać:
\(x^3-\frac{1}{5}\leq 0\)
\(x^3-(\frac{1}{\sqrt[3]{5}})^3\leq 0\)
Otrzymaliśmy nierówność algebraiczną. Wielomian możemy rozłożyć na czynniki, stosując wzór skróconego mnożenia na różnicę sześcianów.
Oznaczenia: \(a\) i \(b\) oznaczają \(a=x, b=\frac{1}{\sqrt[3]{5}}\). Mamy więc:
\(x^3-(\frac{1}{\sqrt[3]{5}})^3\leq 0\)
\((x-\frac{1}{\sqrt[3]{5}})[x^2+\frac{1}{\sqrt[3]{5}}x+(\frac{1}{\sqrt[3]{5}})^2]\leq 0\)
\(x_1=\frac{1}{\sqrt[3]{5}}\)
Mamy tylko jeden pierwiastek. Sporządzamy siatkę znaków. Miejsca zerowe wyznaczają przedziały, które zapisujemy w kolumnach. W rzędach zapisujemy czynniki wielomianu. Ostatni wiersz, to znaki wielomianu. W kratkach zapisujemy znaki czynników dla wartości z poszczególnych przedziałów. Oto tabela:
| \(x\) | \((-\infty;\frac{1}{\sqrt[3]{5}})\) | \(\frac{1}{\sqrt[3]{5}}\) | \((\frac{1}{\sqrt[3]{5}};\infty)\) |
| \(x-\frac{1}{\sqrt[3]{5}}\) | \(-\) | \(0\) | \(+\) |
Jak sprawdzić znak czynnika dla danego przedziału? Wystarczy dowolną liczbę z danego przedziału podstawić za niewiadomą i obliczyć wynik. Znak wyniku wpisujemy do kratki tabeli. (np. dla pierwszej kratki znak ustalamy w następujący sposób: weźmy dowolną liczbę z przedziału , niech to będzie 0 i podstawmy do czynnika wielomianu za \(x\) i otrzymujemy wynik ujemny. Znak "-" wpisujemy do odpowiedniej kratki).
Ponieważ szukamy wartości mniejszych lub równych zero, rozwiązanie nierówności algebraicznej jest następujące:
\(x\in (-\infty;\frac{1}{\sqrt[3]{5}}\rangle\)
Uwzględniając dziedzinę nierówności logarytmicznej (przedział zaznaczony na pomarańczowo) otrzymamy rozwiązanie nierówności logarytmicznej. Szukamy części wspólnej obu zbiorów na osi liczbowej.
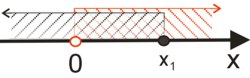
Odpowiedź
© medianauka.pl, 2009-12-20, ZAD-438
Zadania podobne
Zadanie nr 1.
Rozwiązać nierówność logarytmiczną \(\log_{\frac{1}{3}}{x^2}\geq 1\).
Zadanie nr 3.
Rozwiązać nierówność logarytmiczną \(\frac{4\log_{\frac{1}{2}}{x}}{1+\log_{\frac{1}{2}{x}}}\geq 2\).
Zadanie nr 4.
Rozwiązać nierówność logarytmiczną \(\log_{\frac{2}{x+1}}{\frac{1}{3}}>0\).