Zadanie - równanie algebraiczne
Treść zadania:
Rozwiązać równanie wielomianowe \(x^6-6x^5+x^4+16x^3+15x^2+22x+15=0\).
 Rozwiązanie zadania
Rozwiązanie zadania
Aby rozwiązać to równanie należy wielomian występujący po lewej stronie równania doprowadzić do postaci iloczynowej. Szukamy pierwiastków wielomianu wśród podzielników wyrazu wolnego, a więc wśród liczb: \(1,-1,3,-3,5,-5, 15 i -15\).
Obliczamy wartość wielomianu dla tych liczb:
\(W=x^6-6x^5+x^4+16x^3+15x^2+22x+15\_
\(W(1)=1^6-6\cdot 1^5+1^4+16\cdot 1^3+15\cdot 1^2+22\cdot 1+15=\)
\(=1-6+1+16+15+22+15=64\neq 0\)
\(W(-1)=1+6+1-16+15-22+15=0\)
\(W(3)=729-6\cdot 243+81+16\cdot 27+15\cdot 9 +22\cdot 3+15=\)
\(=729-1458+81+432+135+66+15=0\)
\(W(-3)=729+1458+81-432+135-66+15\neq 0\)
\(W(5)=15625-6\cdot 3125+625+16\cdot 125+15\cdot 25 +22\cdot 5+15=\)
\(=15625-18750+625+2000+375+110+15=0\)
\(W(-5)=15625+18750+625-2000+375-110+15\neq 0\)
Można jeszcze obliczyć wartość wielomianu dla \(15\) i \(-15\), jednak mając już trzy pierwiastki wielomianu można poszukać pozostałych pierwiastków potem. Będzie to prawdopodobnie łatwiejsze, gdyż teraz potęga wielomianu jest wysoka i rachunki byłyby uciążliwe.
Skoro liczby \(-1, 3\) i \(5\) są pierwiastkami wielomianu \(W(x)\), to zgodnie z twierdzeniem Bezout wielomian \(W(x)\) dzieli się bez reszty przez \(x+1, x-3, x-5\). Dzieli się też bez reszty przez iloczyn tych jednomianów. Możemy najpierw podzielić \(W(x)\) przez \(x+1\), potem wynik przez kolejny jednomian i tak dalej, jednak efekt osiągniemy szybciej, gdy od razu podzielimy wielomian \(W(x)\) przez iloczyn tych jednomianów.
\((x+1)(x-3)(x-5)=(x^2-3x+x-3)(x-5)=\)
\(=(x^2-2x-3)(x-5)=x^3-5x^2-2x^2+10x-3x+15=\)
\(=x^3-7x^2+7x+15\)
Wykonujemy dzielenie wielomianów:
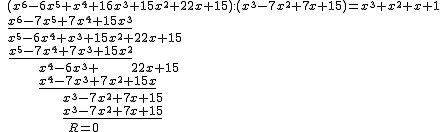
Podkreślenia w powyższym działaniu oznaczaniu oznacza różnicę wielomianów.
Teraz dalej możemy rozkładać wielomian \(x^3+x^2+x+1\) na czynniki. Szukamy wśród podzielników wyrazu wolnego: \(1\), a więc wśród liczb \(1\) i \(-1\).
\(W_1(x)=x^3+x^2+x+1\)
\(W_1(1)=1+1+1+1=4\)
\(W_1(-1)=-1+1-1+1=0\)
Wykonujemy więc jeszcze dzielenie wielomianu \(W_1(x)\) przez \(x+1\).
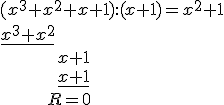
Dwumian \(x^2+1\) nie rozkłada się już na czynniki (\(\Delta=b^2-4ac=0-4\cdot 1\cdot 1=-4<0\)
Możemy więc zapisać, że:
\(x^6-6x^5+x^4+16x^3+15x^2+22x+15=\)
\(=(x+1)(x+1)(x-3)(x-5)(x^2+1)=\)
\(=(x+1)^2(x-3)(x-5)(x^2+1)\)
Równanie wielomianowe ma więc 3 rozwiązania:
 Odpowiedź
Odpowiedź
© medianauka.pl, 2009-12-28, ZAD-450


Zadania podobne
Zadanie nr 1.
Rozwiązać równanie wykładnicze \((\frac{1}{2})^{x-1}-2^{2x}-1=0\).
Zadanie nr 2.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{3x^2-2x+1}{2x^3-3x^2-2x}\).
Zadanie nr 3.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{x^4-x^3+x^2+6x-1}{6x^3-5x^2-2x+1}\)
Zadanie nr 6.
Dla jakich wartości parametrów \(a\) i \(b\) równanie \(x^4-6x^3+10x^2-bx+a=0\) ma podwójny pierwiastek, równy 3?

Zadanie nr 10 — maturalne.
Suma wszystkich pierwiastków równania \((x+3)(x+7)(x-11)=0\) jest równa:
A. \(-1\)
B. \(21\)
C. \(1\)
D. \(-21\)

Zadanie nr 11 — maturalne.
Wspólnym pierwiastkiem równań \((x^2-1)(x-10)(x-5)=0\) i \(\frac{2x-10}{x-1}=0\) jest liczba:
A. -1
B. 1
C. 5
D. 10

Zadanie nr 15 — maturalne.
Suma wszystkich rozwiązań równania \(x(x−3)(x+2)=0\) jest równa
A. 0
B. 1
C. 2
D. 3

Zadanie nr 17 — maturalne.
Iloczyn wszystkich rozwiązań równania \(2x(x^2-9)(x+1)=0\) jest równy
A. -3
B. 3
C. 0
D. 9

Zadanie nr 18 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Jednym z rozwiązań równania \(\sqrt{3}(x^2-2)(x+3)=0\) jest liczba
A. 3
B. 2
C. \(\sqrt{3}\)
D. \(\sqrt{2}\)

