Zadanie - Obliczanie granicy niewłaściwej z definicji
Treść zadania:
Wykazać, że \(\displaystyle\lim_{n\to\infty}\sqrt{n}=+\infty\).
 Rozwiązanie zadania
Rozwiązanie zadania
Ciąg jest rozbieżny do nieskończoności. Zgodnie z definicją granicy niewłaściwej ciągu musimy wykazać, że dla dowolnej liczby rzeczywistej \(M\) prawie wszystkie wyrazy tego ciągu są większe od tej liczby.
Mamy ciąg \(a_n=\sqrt{n}\). Wypiszmy kilka pierwszych wyrazów tego ciągu:
\(a_1=1\)
\(a_2=\sqrt{2}\)
\(a_3=\sqrt{3}\)
\(a_4=2\)
\(a_5=\sqrt{5}\)
\(...\)
Zakładamy więc, że \(M\) jest dowolną liczbą rzeczywistą i badamy, dla jakiej wartości \(n_0\):
\(a_n>M\)
\(\sqrt{n}>M\)
Liczba \(n\) jest dodatnia, załóżmy natomiast, że \(M\) jest też dodatnie. Możemy wówczas podnieść obie strony nierówności do kwadratu, otrzymamy \(n>M^2\). Zatem dla dowolnej liczby rzeczywistej \(M\), począwszy od \(n_0\)-tego (\(n_0>M^2\)) wyrazu ciągu \((a_n)\) prawie wszystkie wyrazy ciągu są większe od liczby \(M\).
Zauważamy, że jeżeli \(M\) jest liczbą ujemną, to ponieważ pierwiastek jest zawsze dodatni, wszystkie wyrazy ciągu są większe od liczby \(M\).
Zgodnie z definicją granicą tego ciągu jest nieskończoność.
Aby lepiej zrozumieć to rozwiązanie, to zastosujemy kilka przykładów:
Niech np. \(M=-5\). Spójrz teraz na wyrazy ciągu, jakie wypisaliśmy na początku. Widać, że wszystkie wyrazy ciągu są większe od \(-5\).
Niech np. \(M=2\). Zgodnie z naszymi wyliczeniami dla \(n_0>M^2=4\) prawie wszystkie wyrazy ciągu są większe od \(M\). I rzeczywiście, dopiero dla \(n_0=5\) prawie wszystkie wyrazy ciągu, czyli wszystkie za wyjątkiem wyrazu \(1, 2, 3, 4\)-ego są większe od \(2\).
© medianauka.pl, 2010-01-02, ZAD-480


Zadania podobne
Zadanie nr 1.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{-n^2-4n+1}{n^2+2}-5)\).
Zadanie nr 2.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)\).
Zadanie nr 3.
Wykazać na podstawie definicji granicy niewłaściwej, że \(\displaystyle\lim_{n\to\infty}(1+2n)=+\infty\).
Zadanie nr 4.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{1-n^2}{n}=-\infty\).
Zadanie nr 6.
Wykazać na podstawie definicji, że \(\displaystyle\lim_{n\to\infty}\frac{2n+3}{n}=2\).
Zadanie nr 7.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}\frac{1+2+3+...+n}{n^2+n-1}\).

Zadanie nr 8 — maturalne.
Granica \(\displaystyle\lim_{n\to \infty}{\frac{(pn^2+4n)^3}{5n^6-4}}=-\frac{8}{5}\). Wynika stąd, że
A. \(p=-8\)
B. \(p=4\)
C. \(p=2\)
D. \(p=-2\)

Zadanie nr 9 — maturalne.
Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie nr 10 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(\frac{3n^2+7n-5}{11-5n+5n^2}\) dla każdej liczby naturalnej \(n\geq 1\). Granica tego ciągu jest równa
A. \(3\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{5}\).
D. \(-\frac{5}{11}\).

Zadanie nr 11 — maturalne.
Oblicz granicę
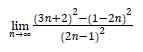 .
.
W poniższe kratki wpisz kolejno – od lewej do prawej – cyfrę jedności i pierwsze dwie cyfry po
przecinku skończonego rozwinięcia dziesiętnego otrzymanego wyniku.


Zadanie nr 12 — maturalne.
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\) wzorem \(a_n=\frac{(7p-1)n^3+5pn-3}{(p+1)n^3+n^2+p}\), gdzie \(p\) jest liczbą rzeczywistą dodatnią. Oblicz wartość \(p\), dla której granica ciągu \(a_n\) jest równa \(\frac{4}{3}\). W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.


