Zadanie - równanie algebraiczne (wielomianowe)
Treść zadania:
Rozwiązać równanie \(8x^3-10x^2+x+1=0\).
 Rozwiązanie zadania
Rozwiązanie zadania
Trzeba znaleźć pierwiastki danego wielomianu (oznaczmy go przez \(W(x)\)), co oznacza, że rozwiązujemy równanie algebraiczne.
Pierwiastków szukamy najpierw pośród podzielników wyrazu wolnego, czyli wśród liczb 1 i -1. Sprawdzamy, czy są to pierwiastki wielomianu poprzez zwykłe podstawienie:
\(W(1)=8\cdot 1^3+10\cdot 1^2+1+1=8-10+1+1=0\)
Wartość wielomianu dla \(x=1\) jest równa zeru, więc znaleźliśmy jeden pierwiastek \(x_1=1\). Teraz w celu znalezienia kolejnych pierwiastków podzielimy wielomian \(W(x)\) przez wielomian \((x-1)\). Wykonujemy dzielenie:
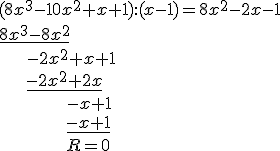
Reszta z dzielenia jest równa zero. Możemy więc nasze równanie zapisać w postaci:
\((x-1)(8x^2-2x-1)=0\)
Mamy jeszcze trójmian kwadratowy, który spróbujemy rozłożyć na czynniki, obliczając wyróżnik trójmianu kwadratowego:
\(8x^2-2x-1\)
\(a=8,\ b=-2,\ c=-1\)
\(\Delta=b^2-4ac=4+32=36\)
\(\sqrt{\Delta}=6\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-6}{16}=-\frac{1}{4}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{2+6}{16}=\frac{1}{2}\)
Trójmian kwadratowy ma 2 pierwiastki. Zatem badane równanie ma trzy rozwiązania.
 Odpowiedź
Odpowiedź
© medianauka.pl, 2010-01-22, ZAD-534


Zadania podobne
Zadanie nr 1.
Rozwiązać równanie wykładnicze \((\frac{1}{2})^{x-1}-2^{2x}-1=0\).
Zadanie nr 2.
Rozwiązać równanie wielomianowe \(x^6-6x^5+x^4+16x^3+15x^2+22x+15=0\).
Zadanie nr 3.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{3x^2-2x+1}{2x^3-3x^2-2x}\).
Zadanie nr 4.
Wyznaczyć dziedzinę funkcji \(f(x)=\frac{x^4-x^3+x^2+6x-1}{6x^3-5x^2-2x+1}\)
Zadanie nr 6.
Dla jakich wartości parametrów \(a\) i \(b\) równanie \(x^4-6x^3+10x^2-bx+a=0\) ma podwójny pierwiastek, równy 3?

Zadanie nr 10 — maturalne.
Suma wszystkich pierwiastków równania \((x+3)(x+7)(x-11)=0\) jest równa:
A. \(-1\)
B. \(21\)
C. \(1\)
D. \(-21\)

Zadanie nr 11 — maturalne.
Wspólnym pierwiastkiem równań \((x^2-1)(x-10)(x-5)=0\) i \(\frac{2x-10}{x-1}=0\) jest liczba:
A. -1
B. 1
C. 5
D. 10

Zadanie nr 15 — maturalne.
Suma wszystkich rozwiązań równania \(x(x−3)(x+2)=0\) jest równa
A. 0
B. 1
C. 2
D. 3

Zadanie nr 17 — maturalne.
Iloczyn wszystkich rozwiązań równania \(2x(x^2-9)(x+1)=0\) jest równy
A. -3
B. 3
C. 0
D. 9

Zadanie nr 18 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Jednym z rozwiązań równania \(\sqrt{3}(x^2-2)(x+3)=0\) jest liczba
A. 3
B. 2
C. \(\sqrt{3}\)
D. \(\sqrt{2}\)

