Zadanie - nierówność kwadratowa z parametrem
Treść zadania:
Dla jakich wartości parametru \(m\) nierówność \(x^2-2x-m+1\leq 0\) ma jedno rozwiązanie \(x=1\)?
 Rozwiązanie zadania
Rozwiązanie zadania
Nierówność kwadratowa o dodatnim współczynniku \(a\) (liczbie przy \(x^2\)) będzie miała jedno rozwiązanie tylko w przypadku pokazanym na rysunku:
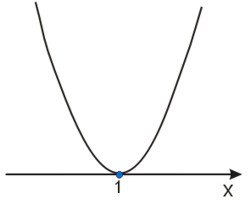
Dlaczego? Dlatego, że szukamy wartości mniejszych od zera (tutaj takich nie ma) oraz równych zero (tutaj tylko dla \(x=1\)). Zatem mamy szukane rozwiązanie \(x=1\). aby trójmian miał jedno miejsce zerowe wyróżnik trójmianu musi być równy zeru.
Obliczamy wyróżnik:
\(a=1,\ b=-2,\ c=-m+1\)
\(\Delta=b^2-4ac=(-2)^2-4\cdot 1\cdot (-m+1)=\)
\(=4-4(1-m)=4-4+4m=4m\)
Wyróżnik musi być równy zeru, więc:
\(\Delta=4m=0/:4\)
\(m=0\)
Dla \(m=0\) dostajemy nierówność:
\(x^2+2x+1\leq 0\)
\(x_0=-\frac{b}{2a}=-\frac{-2}{2}=1\)
Potwierdziliśmy, że dla \(m=0\) trójmian ma jeden pierwiastek \(x=1\), a nierówność ma tylko jedno rozwiązanie: \(x=1\).
 Odpowiedź
Odpowiedź
© medianauka.pl, 2010-02-11, ZAD-594


Zadania podobne
Zadanie nr 1.
Dla jakiej wartości parametru \(x\) prawdziwa jest równość \(\sqrt{(x^2-2x+1)^2}=x^2-2x+1\)?
Zadanie nr 4.
Rozwiązać nierówność:
a) \(x^2+2x-3\geq 0\)
b) \(-x^2+\frac{3}{4}x-\frac{1}{8}> 0\)
c) \(-x^2+2\leq 0\)
Zadanie nr 5.
Rozwiązać nierówność:
a) \(\sqrt{3}x^2+\sqrt{2}x+1< 0\)
b) \(-x^2-2x-5\geq 0\)
Zadanie nr 6.
Rozwiązać nierówność:
a) \(x^2+8x+16> 0\)
b) \(-x^2+2\sqrt{2}x-2\geq 0\)
Zadanie nr 7.
Dla jakich wartości parametru \(m\) zbiorem rozwiązań nierówności \(x^2+mx-1+m> 0\) jest:
a) zbiór liczb rzeczywistych?
b) zbiór pusty?


