Równania Maxwella

Równania Maxwella albo prawa Maxwella to cztery podstawowe równania, za pomocą których można opisać własności pola magnetycznego i elektrycznego. To podstawowe równania elektromagnetyzmu, które wyraża się w postaci całkowej lub w postaci różniczkowej.

Poziom zaawansowany

Równania Maxwella wymagają znajomości matematyki wyższej. Rzadko wyraża się je w innej postaci.

Lp.	Postać całkowa	Postać różniczkowa	Nazwa	Opis
1.	\(\oint_{L}{\vec{E}\cdot}d\vec{l}=-\frac{d\Phi_B}{dt}\)	\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\) lub \(rot\vec{E}=-\frac{\partial \vec{B}}{\partial t}\)	Uogólnione prawo indukcji Faradaya	Zmienne pole magnetyczne wytwarza wirowe pole elektryczne.
2.	\(\oint_{L}{\vec{H}\cdot}d\vec{l}=I+\frac{d\Phi_D}{dt}\)	\(\nabla \times \vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}\) lub \(rot \vec{H}=\vec{j}+\frac{\partial \vec{D}}{\partial t}\)	Uogólnione prawo Ampere'a	Zmienne pole elektryczne i prąd elektryczny wytwarzają wirowe pole magnetyczne.
3.	\(\oint_{S}{\vec{D}\cdot}d\vec{S}=Q\) lub \(\oint_{S}{\vec{D}\cdot}d\vec{S}=\int_{V}\rho dV\)	\(\nabla \cdot \vec{D}=\rho\) lub \(div \vec{D}=\rho\)	Prawo Gaussa dla pola elektrycznego	Źródłem pola elektrycznego jest ładunek Q.
4.	\(\oint_{S}{\vec{B}\cdot}d\vec{S}=0\)	\(\nabla \cdot \vec{B}=0\) lub \(div \vec{B}=0\)	Prawo Gaussa dla pola magnetycznego	Pole magnetyczne jest bezźródłowe.

Powyższe równania mogą jeszcze przyjmować inne postaci, z uwzględnieniem zależności:

\(\vec{D}=\epsilon \vec{E}\)

\(\vec{B}=\mu \vec{H}\)

A oto oznaczenia symboli, jakie zostały użyte w powyższych wzorach:

\(E\) - natężenie pola elektrycznego,
\(D\) - indukcja elektryczna,
\(B\) - indukcja magnetyczna,
\(H\) - natężenie pola magnetycznego,
\(\Phi_D\) - strumień indukcji elektrycznej,
\(\\Phi_B\) - strumień indukcji magnetycznej,
\(j\) - gęstość prądu,
\(I\) - natężenie prądu,
\(\rho\) - gęstość ładunku elektrycznego,
\(\varepsilon\) - przenikalność elektryczna ośrodka,
\(\mu\) - przenikalność magnetyczna ośrodka,
\(\nabla\) - operator dywergencji,
\(\nabla \times\) - operator rotacji.
\(S\) - dowolna powierzchnia rozpięta na linii zamkniętej \(L\).

Należy pamiętać, że przenikalność elektryczna i magnetyczna są wartościami liczbowymi jedynie dla ośrodków materialnych izotropowych, w tym próżni. W pozostałych przypadkach wielkości te są tensorami, co sprawia, że wektory indukcji i natężenia nie są zawsze równoległe.

Równania Maxwella dla próżni

W próżni równania Maxwella przybierają postać:

\(\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)

\(\nabla \times \vec{B}=\mu_0\epsilon_0\frac{\partial \vec{E}}{\partial t}\)

\(\nabla \cdot \vec{B}=0\)

\(\nabla \cdot \vec{E}=0\)

Wnioski z równań Maxwella

Z równań Maxwella wynikają co najmniej dwa bardzo istotne wnioski:

istnieją fale elektromagnetyczne,
zasada zachowania ładunku.

Ciekawostki

Maxwell przewidział istnienie fal elektromagnetycznych, które Heinrich Hertz odkrył w 1888 roku. Swoje równania sformułował w 1864 roku. Maxwell wywnioskował ze swoich równań, że w próżni zmienne pole magnetyczne wywołuje zmienne pole elektryczne i to z kolei wywołuje znów pole magnetyczne zmienne itd. W 1865 roku Maxwell wyraził pogląd, iż światło może mieć naturę elektromagnetyczną.

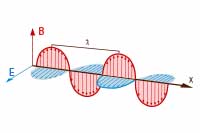Fale elektromagnetyczne

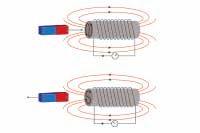Indukcja elektromagnetyczna