Obrazy w soczewkach i równanie soczewki

Zapamiętaj

Równanie soczewki cienkiej ma postać:

\(\frac{1}{x}+\frac{1}{y}=\frac{1}{f}\)

Dla soczewki skupiającej \(f\gt 0\), a dla soczewki rozpraszającej \(f\lt 0\).

Jeżeli \(y\gt 0\), obraz jest rzeczywisty, a jeżeli \(y\lt 0\), obraz jest pozorny.

Wartość powiększenia obrazu można obliczyć ze wzoru:

\(p=\frac{|y|}{x}\)

Soczewka rozpraszająca dla rzeczywistego przedmiotu tworzy zawsze obraz pozorny, prosty i pomniejszony.

Aby skonstruować obraz powstający w soczewce skupiającej, wystarczy narysować co najmniej dwa z trzech charakterystycznych promieni:

promień przechodzący przez środek optyczny soczewki cienkiej biegnie w przybliżeniu bez zmiany kierunku,
promień biegnący równolegle do głównej osi optycznej po przejściu przez soczewkę biegnie przez ognisko po drugiej stronie soczewki,
promień biegnący przez ognisko znajdujące się po stronie przedmiotu po przejściu przez soczewkę biegnie równolegle do głównej osi optycznej.

Powyższe zasady przedstawiamy na przykładowym rysunku.

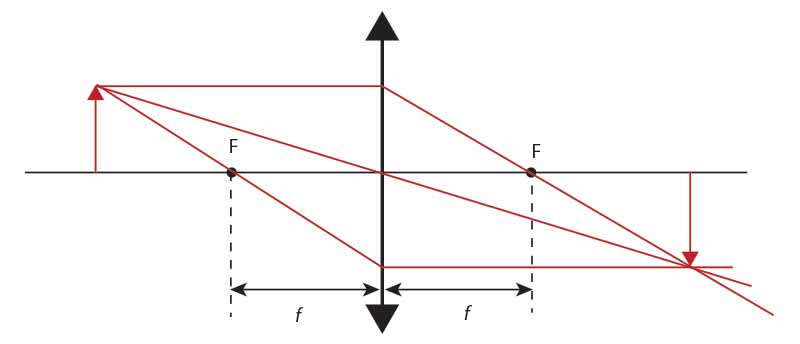
Powstawanie obrazu w soczewce skupiającej - konstrukcja

Równanie soczewki

Przyjmujemy, że dla rzeczywistego przedmiotu \(x\gt 0\). Dla soczewki skupiającej \(f\gt 0\), a dla soczewki rozpraszającej \(f\lt 0\). Jeżeli \(y\gt 0\), obraz jest rzeczywisty, natomiast jeżeli \(y\lt 0\), obraz jest pozorny.

Równanie soczewki jest zależnością matematyczną między odległością przedmiotu od soczewki \(x\), odległością obrazu od soczewki \(y\) a ogniskową soczewki \(f\).

\(\frac{1}{x}+\frac{1}{y}=\frac{1}{f}\)

lub

\(y=\frac{xf}{x-f}\)

Interpretacja wyników:

Jeżeli \(y\lt 0\), to obraz jest pozorny, gdy \(y\gt 0\), to obraz jest rzeczywisty. W soczewkach obrazy pozorne są proste, a rzeczywiste odwrócone.

Wzór na powiększenie obrazu:

\(p=\frac{|y|}{x}\)

Poniższa tabela zestawia różne przypadki powstawania obrazów w soczewkach.

Odległość przedmiotu od soczewki	Rodzaj soczewki	Odległość obrazu od soczewki	Powiększenie	Rodzaj obrazu
\(x\gt 2f\)	skupiająca	\(f\lt y\lt 2f\)	\(p\lt 1\)	pomniejszony rzeczywisty odwrócony
\(x=2f\)		\(y=2f\)	\(p=1\)	tej samej wielkości co przedmiot rzeczywisty odwrócony
\(f\lt x\lt 2f\)		\(y\gt 2f\)	\(p\gt 1\)	powiększony rzeczywisty odwrócony
\(x=f\)		Promienie po przejściu przez soczewkę są równoległe – obraz znajduje się w nieskończoności.
\(0\lt x\lt f\)		\(y\lt 0\)	\(p\gt 1\)	powiększony pozorny prosty
\(x\gt 0\)	rozpraszająca	\(f\lt y\lt 0\)	\(0\lt p\lt 1\)	pomniejszony pozorny prosty

Powstawanie obrazu w soczewce rozpraszającej

Zaprezentujemy jeszcze na ilustracji konstrukcję obrazu w soczewce rozpraszającej.

W soczewce rozpraszającej do konstrukcji obrazu również wystarczą dwa charakterystyczne promienie:

promień przechodzący przez środek optyczny soczewki cienkiej biegnie w przybliżeniu bez zmiany kierunku,
promień biegnący równolegle do głównej osi optycznej po przejściu przez soczewkę rozchodzi się tak, jakby wychodził z ogniska znajdującego się po stronie przedmiotu,
promień skierowany w stronę ogniska znajdującego się po przeciwnej stronie soczewki po przejściu przez soczewkę biegnie równolegle do głównej osi optycznej.

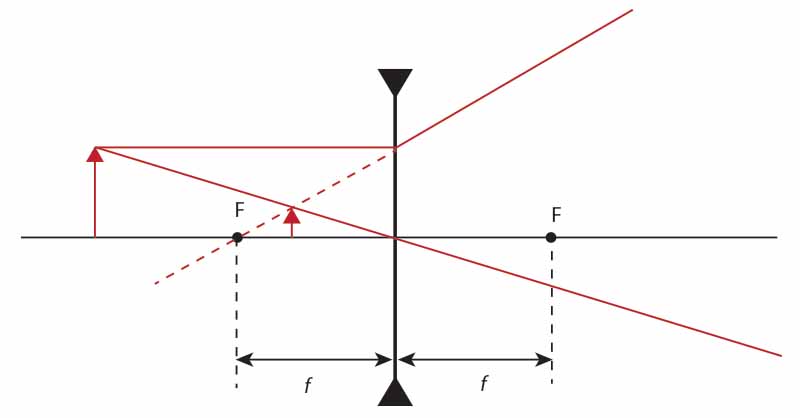
Powstawanie obrazu w soczewce rozpraszającej

Dodatkowe materiały edukacyjne

Laboratorium soczewki — gdzie powstanie obraz? Przeciągaj przedmiot wzdłuż osi optycznej i obserwuj konstrukcję obrazu z promieni charakterystycznych.

Symulacja