Równanie zwierciadła

Równanie zwierciadła kulistego ma następującą postać:

\(\frac{1}{x}+\frac{1}{y}=\frac{1}{f}\)

gdzie:

\(x\) - odległość przedmiotu od zwierciadła,
\(y\) - odległość obrazu od zwierciadła,
\(f\) - ogniskowa zwierciadła.

Aby obliczyć w jakiej odległości od zwierciadła powstanie obraz, wystarczy przekształcić powyższe równanie do innej postaci:

\(y=\frac{xf}{x-f}\)

Jeżeli otrzymamy wartość ujemną \(y\), to oznacza, że otrzymany obraz jest obrazem pozornym. Wartość dodatnia, że obraz jest rzeczywisty. Odległość obrazu od środka zwierciadła będzie wówczas równa \(|y|\).

Równanie zwierciadła kulistego jest prawdziwe dla zwierciadła wklęsłego i wypukłego (\(f\lt 0\)).

Powiększenie obrazu w zwierciadle

Warto jeszcze wprowadzić pojęcie powiększenia obrazu, który z cech podobieństwa trójkątów można wyrazić poprzez odległości przedmiotu i jego obrazu, a nie poprzez ich rozmiary.

Powiększenie obrazu w zwierciadle dane jest wzorem:

\(p=\frac{|y|}{x}\)

Możliwe są następujące przypadki:

\(p=1\) - obraz ma takie same wymiary jak przedmiot,
\(p\lt 1\) - obraz pomniejszony,
\(p\gt 1\) - obraz powiększony.

Wykres

Równanie zwierciadła można zilustrować wykresem:

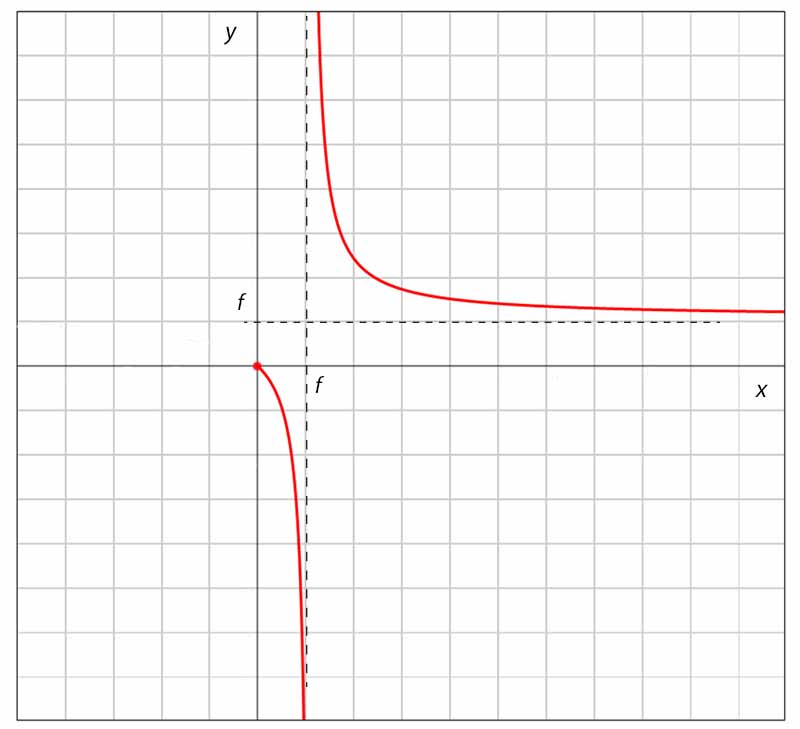
Na podstawie analizy wykresu możemy wyciągnąć następujące wnioski:

Gdy \(0\lt x\lt f\), to \(y\) maleje od zera do minus nieskończoności to mamy do czynienia z obrazem pozorny (\(y\lt 0\)) i powiększonym (\(|y|\gt x\), więc \(p\gt 1\)).
Gdy \(x\gt f\), to obraz jest rzeczywisty (\(y\gt 0\)), najpierw powiększony, a dla \(x\gt 2f\) pomniejszony.
Gdy \(x=2f\), obraz jest rzeczywisty, niepowiększony.

Zwierciadło wypukiłe

Zwierciadło wklęsłe