Rozkład Maxwella

Cząstki gazu w naczyniu poruszają się chaotycznie. Nie ma wyróżnionego żadnego kierunku ruchu cząstek. Jeżeli w danej chwili pojawi się uprzywilejowany kierunek ruchu cząsteczek, to ponieważ jest ich bardzo duzo i następuje bardzo dużo zderzeń, uprzywilejowanie to niemalże od razu znika. Gdyby tak nie było, wszystkie cząstki nagle znalazły by się w jednej części naczynia, a w innej wytworzyłaby siępróżnia. To niemożliwe (w w zasadzie bardzo mało prawdopodobne). A co z wartościami prędkości tych czątek? Czy wszystkie poruszają się tak samo szybko? Nie. Na to pytanie odpowiada tak zwany rozkład Maxwella.

James Clerk Maxwell kierując się założeniami kinetycznej teorii gazu doskonałego sformułował prawo rozkładu prędkości poruszających się cząsteczek.

$f(v)=\frac{4}{\sqrt{\pi}}\frac{v^2}{v_{p}^3} e^{-\frac{v^2}{v_{p}^2}}\\v_p=\sqrt{\frac{2kT}{m}}$

gdzie:

f(v) - funkcja rozkładu prędkości, czyli rozkład prawdopodobieństwa, że na N cząsteczek dN cząsteczek ma prędkości w przedziale od v do v+dv,
v - prędkość bezwzględna cząsteczki,
v_p - prędkość najbardziej prawdopodobna,
k - stała Boltzmanna,
T - temperatura bezwzględna,
m - masa cząsteczki.

Poniższy wykres ilustruje opisany wyżej rozkład prędkości dla tlenu w dwóch różnych temperaturach.

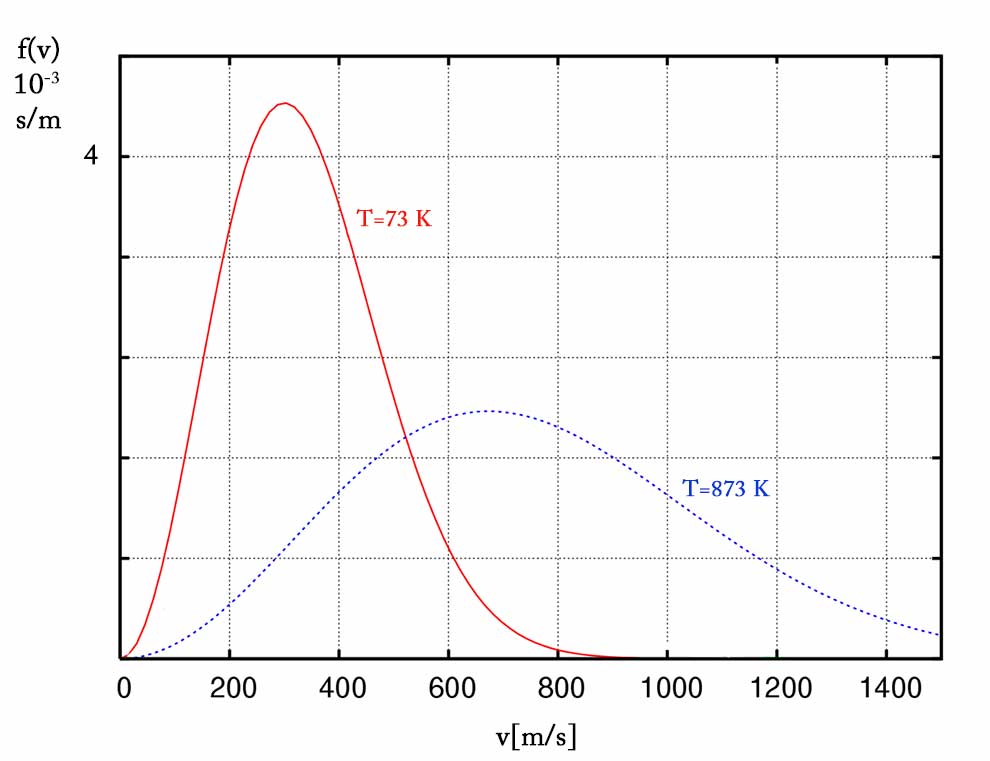
Rozkład Maxwella

Z rozkładu Maxwella można wyznaczyć prędkość średnią:

$\overline v=\int_{\small 0}^{\small \infty}{f(v)}vdv=\sqrt{\frac{8kT}{\pi m}}$

oraz średnią wartośc kwadratu prędkości i prędkość średniąkwadratową:

$\overline v^2=\int_{\small 0}^{\small \infty}{f(v)}v^2dv=\frac{3kT}{m}\\v_{sk}=\sqrt{\frac{3kT}{m}}$

Wnioski

Maksimum krzywej w każdej temperaturze wypada dla wartości v_p. Co to oznacza? Oznacza to tyle, że najwięcej cząsteczek porusza się własnie z taką prędkością.
Z warunek normalizacji
$\int_{\small 0}^{\small \infty}{f(v)}dv=1$
wynika, że pole pod krzywą rozkładu dla danego gazu jest zawsze takie samo.
Wraz ze wzrostem temperatury krzywa wypłaszcza się, a jej maksimum przesuwa się w stronę wyższych wartości prędkości (w prawo).
Rozkład Maxwella jest asymetryczny.
Prędkość średnia cząsteczek jest większa niż prędkośc najbardziej prawdopodobna.
Krzywa Maxwella rozciąga się mocno w stronę wysokich wartości temperatury i wysokich prędkości.
Prędkości cząsteczek w gazie zależne są od masy tych cząsteczek (a tym samym masy molowej). W gazach lżejszych w tej samej temperaturze średnie prędkości cząstek będą wyższe.