Drgania elektromagnetyczne

Rozważmy obwód RLC, jak pokazano na rysunku w sytuacji, w której kondensator o pojemności \(C\) jest naładowany.

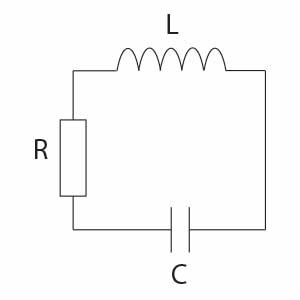
obwód rezonansowy

Na okładkach kondensatora jest pewne napięcie elektryczne, które będzie maleć wraz z rozładowywaniem się kondensatora. Odpływ ładunku elektrycznego z okładek kondensatora powoduje powstanie prądu w obwodzie RLC. Gdy przez cewkę o indukcyjności L płynie prąd elektryczny, zjawisko samoindukcji powoduje powstanie siły elektromotorycznej samoindukcji, która podtrzymuje przepływ prądu nawet wtedy, gdy kondensator jest już całkowicie rozładowany. To podtrzymanie prądu powoduje ponowne naładowanie kondensatora, ale o przeciwnej polaryzacji. Gdy prąd wywołany samoindukcją ustaje, następuje znów rozładowanie kondensatora i cały proces znów się powtarza. W obwodzie powstają drgania elektromagnetyczne. Ponieważ każdy obwód charakteryzuje się pewnym oporem elektrycznym, jest na nim wydzielanie ciepło. Mamy do czynienia ze stratą energii i w efekcie drgania po pewnym czasie ustają. W rzeczywistości zatem w obwodzie RLC mamy do czynienia z drganiami tłumionymi.

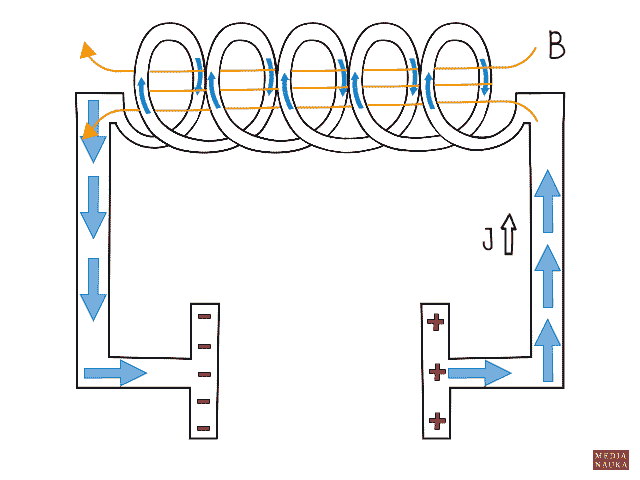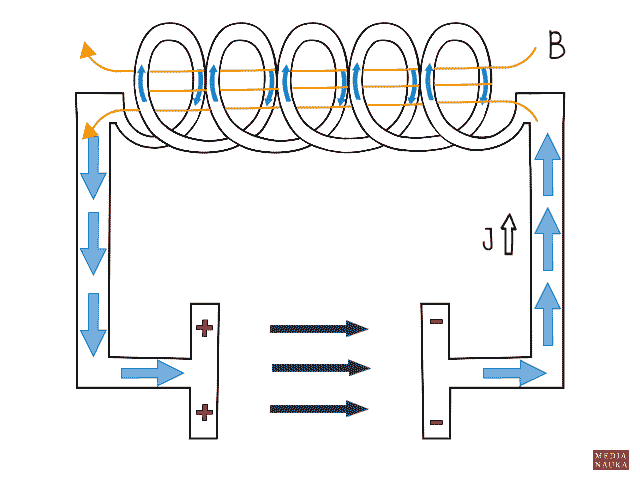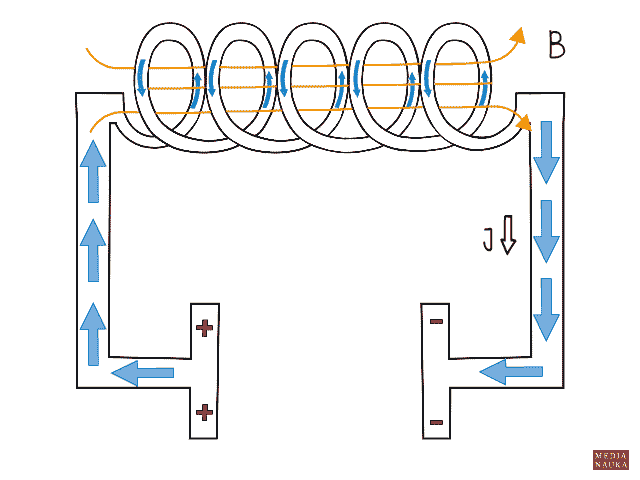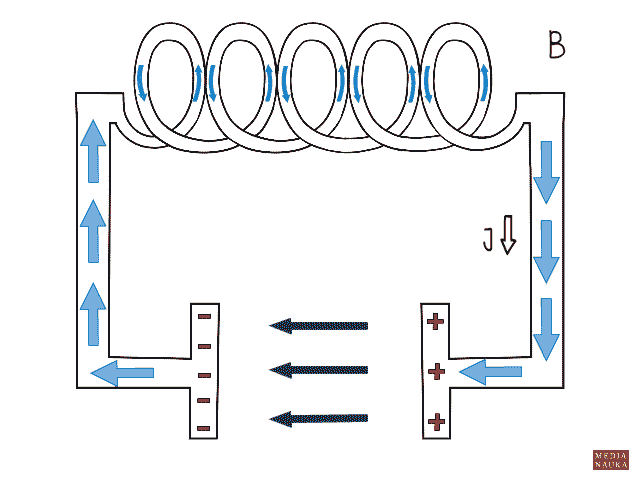
Ewa Trawińska © medianauka.pl

Częstotliwość rezonansowa

Z jaką częstotliwością drga układ RLC?

Impedancja układu RLC jest równa

\(Z=\sqrt{R^2+(R_{L}-R_{C})^2}=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}\)

W sytuacji, w której opór indukcyjny \(R_L\) jest równy oporowi pojemnościowemu \(R_C\) mamy do czynienia z sytuacją, w której impedancja jest równa oporowi \(R\) i nie ma przesunięć fazowych między napięciami na zwojnicy i kondensatorze. Mają wprawdzie przeciwne fazy, ale ich amplitudy są równe. To tak zwany rezonans napięć.

Mamy więc:

\(\omega L-\frac{1}{\omega C}=0\)

\(\omega^2 LC-1=0\)

\(\omega =\frac{1}{\sqrt{LC}}\)

Otrzymany wzór to wzór na częstotliwość rezonansową:

\(\omega_r =\frac{1}{\sqrt{LC}}\)

lub

\(f_r=\frac{1}{2\pi \sqrt{LC}}\)

Częstotliwość rezonansowa w obwodzie RLC to tak zwana częstotliwość drgań własnych obwodu RLC. Co to oznacza? Jeżeli dostarczymy do kondensatora ładunek elektryczny, to układ zacznie wykonywać drgania elektromagnetyczne właśnie z wyznaczoną wyżej częstotliwością.

Przemiana energii

Podczas opisanych wyżej drgań ma miejsce ciągła zamiana energii pola elektrycznego w kondensatorze

\(E_C=\frac{1}{2} \frac{Q^2}{C}\)

na energię pola magnetycznego w zwojnicy

\(E_L=\frac{1}{2}LI^2\)

i odwrotnie.

Dobroć obwodu

Każdy z elementów obwodu stawia prądowi opór, stąd drgania po pewnym czasie wygasają. Wygaszanie drgań charakteryzuje tak zwana dobroć obwodu. Wzór na dobroć obwodu jest następujący:

\(q=\frac{1}{R}\sqrt{\frac{L}{C}}\)

Gdy \(R\) dąży do zera, drgania stają się drganiami nietłumionymi.

Analogia między drganiami w obwodzie LC a drganiami mechanicznymi

Między drganiami mechanicznymi a elektromagnetycznymi w obwodzie LC (lub RLC) zachodzi analogia. Ilustruje to poniższa tabelka.

Drgania obwodu LC	Drgania mechaniczne
\(Q\) - ładunek zgromadzony w kondensatorze	\(x\) - wychylenie z położenia równowagi
\(L\) - indukcyjność zwojnicy	\(m\) - masa
\(\frac{1}{C}\)	\(k\) - współczynnik sprężystości
\(\omega_r =\frac{1}{\sqrt{LC}}\)	\(\omega_r=\sqrt{\frac{k}{m}}\)
\(E_C\) - energia pola elektrycznego	\(E_p\) - energia potencjalna sprężystości (równa \(\frac{kx^2}{2}\))
\(E_L\) - energia pola magnetycznego	\(E_k\) - energia kinetyczna (równa \(\frac{mv^2}{2}\))

Fale elektromagnetyczne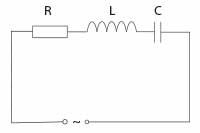

Obwód RLC