Obwód RLC

W obwodach z oporem elektrycznym natężenie prądu i napięcia elektrycznego są zgodne w fazie. Oznacza to, że wartości ekstremalne napięć i natężeń w danej chwili czasu pokrywają się ze sobą.

Spadek napięcia na oporze w obwodzie prądu przemiennego tylko z oporem \(R\) wynosi:

\(U_R=RI\)

W obwodach prądu przemiennego stosuje się ponadto kondensatory (pojemności \(C\)) oraz zwojnice (indukcyjności \(L\)).

Obwód z indukcyjnością

Rozpatrzmy obwód prądu przemiennego jedynie z indukcyjnością.

Poziom zaawansowany

Spadek napięcia na cewce wynosi:

\(U_L=L\frac{dI}{dt}\)

Wiedząc, że \(I=I_0\sin{\omega t}\), otrzymujemy następujący wzór na spadek napięcia na cewce:

\(U_L=I_0\omega L\cos{\omega t}=I_0\omega L\sin{(\omega t+\frac{\pi}{2})}\)

Na cewce zachodzi spadek napięcia:

\(U_L=I_0\omega L\cos{\omega t}=I_0\omega L\sin{(\omega t+\frac{\pi}{2})}\)

Widać, że napięcie i natężenie prądu w obwodzie z indukcyjnością nie jest zgodne w fazie. Napięcie wyprzedza natężenie w fazie o kąt \(\frac{\pi}{2}\).

Opór indukcyjny \(R_L\) (lub \(X_L\)) jest równy:

\(R_L=\frac{U_0}{I_0}=\omega L = 2\pi fL\)

i zależy od indukcyjności cewki oraz od częstotliwości prądu w obwodzie.

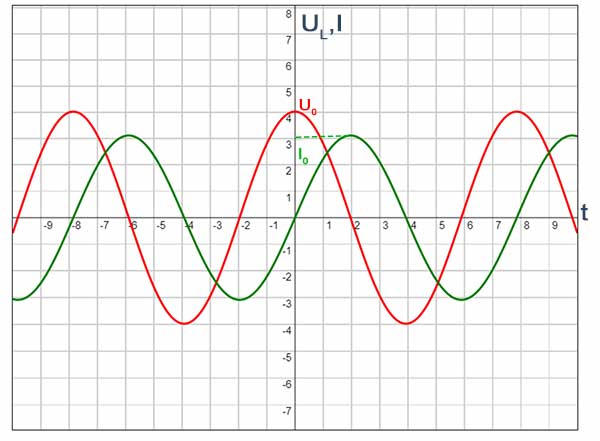
Poniższy wykres przedstawia zależność spadku napięcia na cewce (czerwony wykres) i natężenia prądu (zielony wykres) w obwodzie prądu przemiennego tylko z indukcyjnością.

Napięcie i natężenie w obwodzie prądu przemiennego z indukcyjnością

Obwód z pojemnością

Rozpatrzmy obwód prądu przemiennego z pojemnością \(C\).

Napięcie na kondensatorze o pojemności \(C\) będzie równe \(U_C=\frac{Q}{C}\).

Poziom zaawansowany

Ponadto:

\(U_C=-\frac{1}{C}\int{Idt}\)

Wiedząc, że \(I=I_0\sin{\omega t}\), otrzymujemy następujący wzór na spadek napięcia na pojemności:

\(U_C=-\frac{1}{\omega C}I_0\cos{\omega t}=-\frac{1}{\omega C}I_0\sin{(\omega t-\frac{\pi}{2})}\)

Widać, że napięcie i natężenie prądu w obwodzie prądu przemiennego nie jest zgodne w fazie. Napięcie jest opóźnione w stosunku do natężenia w fazie o kąt \(\frac{\pi}{2}\).

Opór pojemnościowy \(R_C\) (lub \(XC\)) jest równy:

\(R_C=\frac{U_0}{I_0}=\frac{1}{\omega C}=\frac{1}{2\pi f C}\)

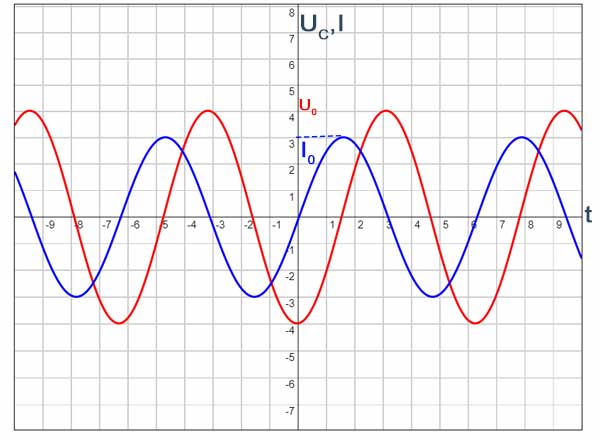
Poniższy wykres przedstawia zależność spadku napięcia na pojemności (czerwony wykres) i natężenia prądu (niebieski wykres) w obwodzie prądu przemiennego tylko z pojemnością.

Napięcie i natężenie w obwodzie prądu przemiennego z pojemnością

Obwody RLC

Obwodami RLC nazywamy obwody, które mogą zawierać elementy R, L i C połączone w różny sposób, a także jedynie R i L lub R i C.

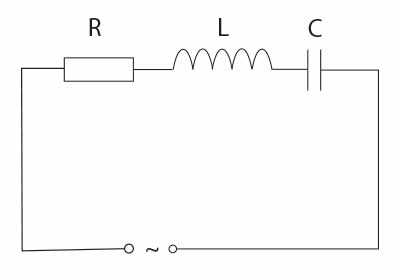
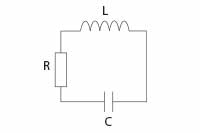
Najprostszy obwód RLC, w którym elementy R, L i C są połączone szeregowo, pokazano na rysunku.

obwód RLC

Napięcie źródła prądu przemiennego będzie równe:

\(U=U_R+U_L+U_C\)

Natężenie prądu przemiennego sinusoidalnie zmienia się w czasie jak: \(I=I_0\sin{\omega t}\).

Napięcie \(U\) przyjmuje postać:

\(U=U_0\sin{(\omega t+\phi)}\)

gdzie \(\phi\) jest przesunięciem fazowym między napięciem a natężeniem prądu w obwodzie RLC, zależne od oporu \(R\), impedancji \(L\) i pojemności \(C\), a także od częstotliwości zmian prądu.

Diagram wskazowy

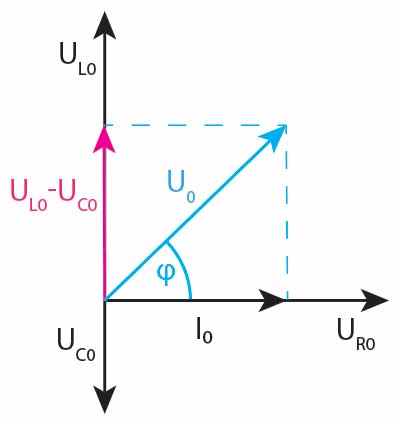
Diagram wskazowy, lub wskaz, jest to graficzny sposób, który pozwala wyznaczyć przesunięcie fazowe w obwodzie RLC. Używa się tu strzałek (nie wektorów) w następujący sposób:

Długość strzałki jest równa wartości amplitudy \(U\) lub \(I\). Kierunek spadku \(U_R\) i prądu \(I\) jest oznaczany na diagramie w prawo. \(U_L\) pionowo w górę, \(U_C\) - pionowo w dół. Kąt między strzałką napięcia (sumą wszystkich napięć) a strzałką prądu jest szukanym kątem przesunięcia fazowego.

Przyjrzyj się poniższej ilustracji, aby to zrozumieć.

diagram wskazowy

Powyższe przesunięcie fazowe można wyliczyć na podstawie wzoru:

\(tg\phi=\frac{R_L-R_C}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}\)

Amplituda napięcia dana jest wzorem:

\(U_0=\sqrt{U_{R0}^2+(U_{L0}-U_{C0})}\)

Impedancja, zawada, reaktancja

Impedancja albo zawada \(Z\) jest to całkowity opór obwodu prądu przemiennego. Wzór na impedancję w obwodzie RLC jest następujący:

\(Z=\sqrt{R^2+(R_{L}-R_{C})^2}\)
\(Z=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}\)

Zauważmy, że gdy w obwodzie RLC popłynie prąd stały, impedancja przechodzi w rezystancję \(Z=R\), gdyż wówczas \(R_L=0\) i \(R_C=0\).

Czasem przez \(X\) oznaczamy wielkość \(R_L-R_C\). To tak zwana reaktancja, czyli opór bierny. Wówczas zawada jest dana wzorem:

\(Z=\sqrt{R^2+X^2}\)

Przez impedancję rozumie się także stosunek wartości skutecznych napięcia i natężenia prądu zmiennego.

\(Z=\frac{U_{sk}}{I_{sk}}\)

Drgania elektromagnetyczne