Krzywe Lissajous

Krzywa Lissajous to krzywa parametryczna, zakreślana przez punkt materialny, który porusza się ruchem harmonicznym w dwóch prostopadłych kierunkach.

Krzywe Lissajous opisuje układ równań:

\(\begin{cases} x(t)=A_1sin(\omega_{1}t+\phi)\\y(t)=A_{2}sin(\omega_{2}t) \end{cases} \)

Parametr \(\phi\) może występować zamiast w pierwszym - w drugim równaniu.

Kształt krzywej opisanej powyższymi równaniami silnie zależy od częstości kołowych \(\omega\) oraz czynnika \(\phi\) W szczególnych przypadkach krzywą Lissajous może być odcinek, elipsa lub okrąg.

Symulacja

Poniżej znajduje się symulacja układu, który wykreśla krzywe Lissajous w zależności od rożnych parametrów równań.

W symulacji przyjęto oznaczenia: fi = φ, p = ω₁:ω₂

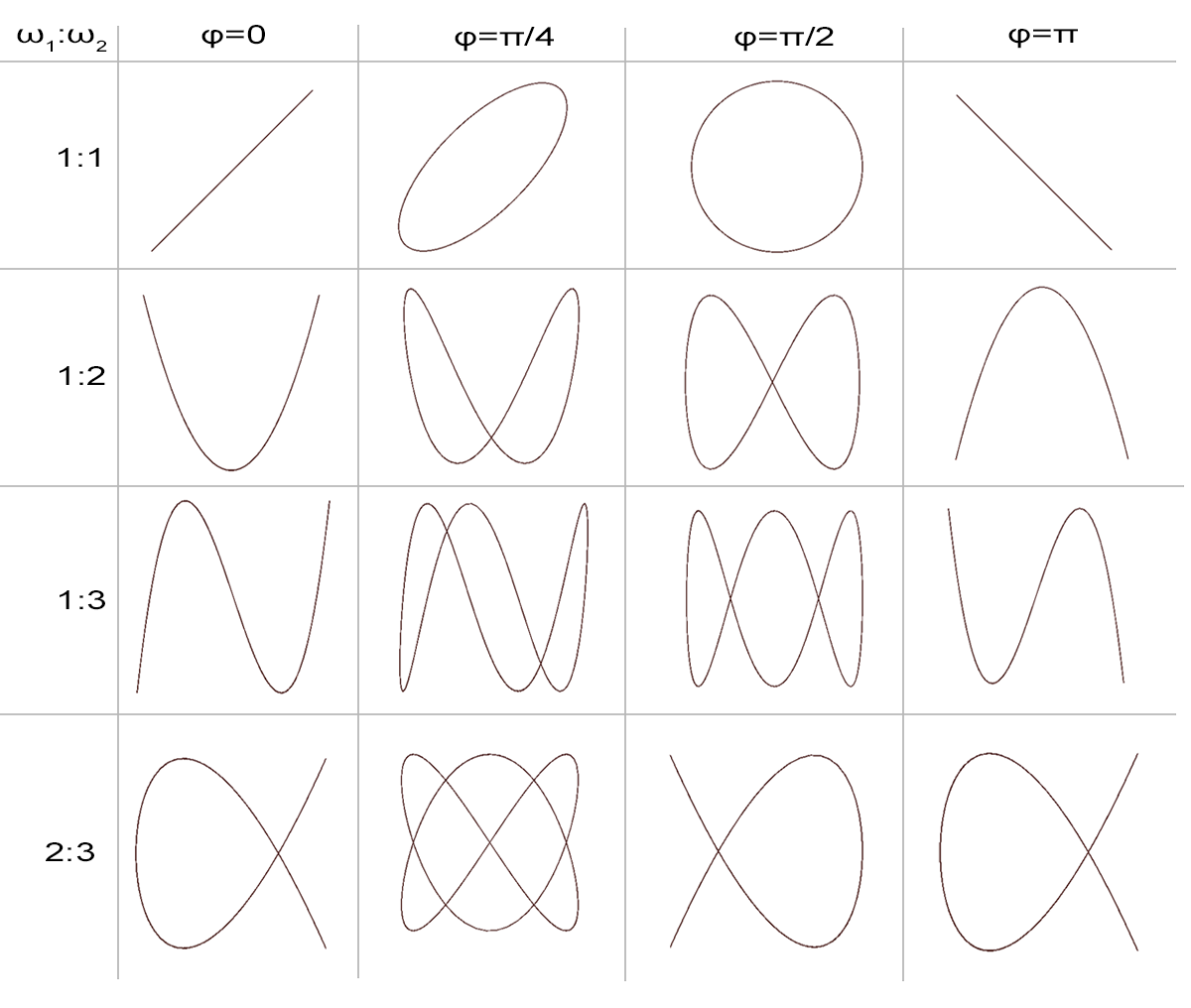
Na poniższym rysunku uwidoczniono wybrane krzywe Lissajous w ujęciu tabelarycznym.

Krzywe Lissajous