Ruch harmoniczny

Zapamiętaj

Ruch harmoniczny - ruch opisany równaniem: x = Acos(ωt+φ)
lub F_x=-kx

A - amplituda drgań,
ω - częstość kątowa drgań,
φ₀ - faza początkowa

Okres drgań harmonicznych

$T=\frac{2\pi}{\omega}$

Częstotliwość drgań

$f=\frac{1}{T}=\frac{\omega}{2\pi}$

Prędkość i przyspieszenie w ruchu harmonicznym:

v = -Aωsin(ωt+φ)
a = -Aω²cos(ωt+φ)
a = -ω²x

Ruch drgający, drganie, oscylacja - jest to taki ruch ciała,

który zachodzi wokół stałego położenia równowagi.

Ruch taki może być okresowy (periodyczny), czyli taki, w którym stan ciała powtarza się w jednakowych odstępach czasu, nazywanych okresem drgań. Okres drgań oznaczamy literą T i mierzymy w sekundach.

Często mamy też do czynienia z ruchem nieokresowym, czyli takim, który nie jest ruchem periodycznym.

Przykład

Ruch drgający jest w przyrodzie wszechobecny. Przykładem oscylacji jest na przykład ruch huśtawki wychylonej z położenia równowagi, ruch wahadła zegara, ruch ciężarka zawieszonego na sprężynie, drganie struny w gitarze, ruch elektronu w obwodzie prądu zmiennego itd.

Opis matematyczny

Zależność położenia punktu materialnego na osi x w chwili t możemy oznaczyć przez

x(t)=x(t+T)

Powyższy zapis oznacza, że położenie punktu w chwili t=t₀ i t=t₀+T jest takie samo (T jest okresem drgań), czyli powtarza się co pewien czas równy T.

Jakiej funkcji można użyć do opisu takiego ruchu? Można użyć praktycznie dowolnej funkcji okresowej, najczęściej jednak korzystamy z funkcji trygonometrycznej cosinus.

Drgania harmoniczne

Drgania opisane poniższym równaniem zależności położenia punktu materialnego x od czasu t nazywamy draniami harmonicznymi.

x=Acos(ωt+φ)

gdzie:

A - amplituda drgań (największe wychylenie z położenia równowagi)
ω - częstotliwość (częstość) kątowa drgań, pulsacja
ωt+φ - faza drgań, w szczególności dla t=0, faza drgań jest równa φ - jest to tak zwana faza początkowa.

Warto dodać, że do wyrażenia ruchu harmonicznego można użyć także funkcji sinus. Wówczas mamy: x=Asin(ωt+φ_s), gdzie φ_s=φ+π/2.

Wykres ruchu harmonicznego

Poniższy rysunek ilustruje jak wygląda wykres zależności x(t) w ruchu harmonicznym, uwzględniając przypadek niezerowej fazy początkowej.

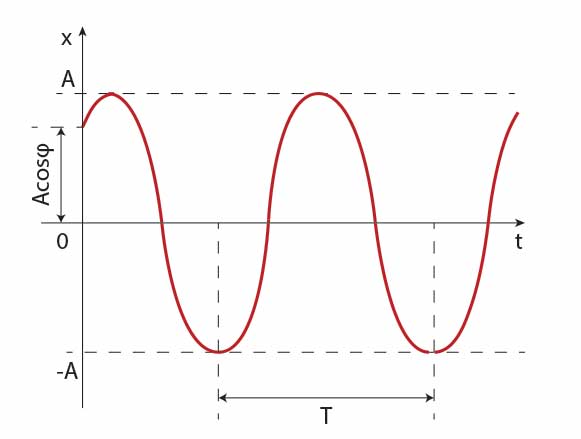
Skąd się wziął powyższy wzór i wykres? Wszystko przez analogię między ruchem jednostajnym po okręgu a ruchem harmonicznym.

Analogia między drganiami harmonicznymi a ruchem po okręgu

Istnieje bardzo duże podobieństwo między wspomnianymi rodzajami ruchu. Ruch po okręgu można potraktować jako złożenie prostopadłych drań harmonicznych, co wyraźnie widać w poniższej symulacji.

Ujęcie dynamiczne

Można jeszcze inaczej zdefiniować ruch harmoniczny. Oto definicja uwzględniająca siłę działającą na rozpatrywane ciało.

Ruch harmoniczny to taki ruch, w którym działająca na ciało siła jest proporcjonalna do wychylenia i przeciwnie do niego zwrócona.

Składowa x wektora siły dana jest wzorem:

F_x=-kx

gdzie

k - stała sprężystości, zależny od materiału (np. sprężyny).
F_x - składowa x siły działającej na ciało
x - współrzędna (wychylenie) ciała na osi.

Okres drgań harmonicznych

Okres drgań harmonicznych to czas, jaki jest potrzebny do zakończenia jednego pełnego cyklu drgania harmonicznego

W ruchu harmonicznym okres drgań jest dany wzorem:

$T=\frac{2\pi}{\omega}$

Poziom zaawansowany

Wyprowadzenie okresu drgań.

Korzystając ze wzorów x(t)=x(t+T) oraz x=Acos(ωt+φ) otrzymujemy:

Acos(ωt+φ)=Acos[ω(t+T)+φ]=Acos(ωt+ωT+φ)

Ponieważ okresem funkcji cosinus jest liczba 2π, bo cosx=cos(x+2π), to z powyższego wzoru wynika, że:

ωT=2π, czyli

T=2π/ω

Związek częstości kątowej drgań z częstotliwością drgań jest następujący:

$f=\frac{1}{T}=\frac{\omega}{2\pi}$

Jednostką częstotliwość jest 1 herc : 1 Hz = 1 s^-1

Prędkość i przyspieszenie w ruchu harmonicznym

Wzór na prędkość w ruchu harmonicznym:

v = -Aωsin(ωt+φ)

Wzór na przyspieszenie w ruchu harmonicznym:

a = -Aω²cos(ωt+φ)

Z porównania powyższego wzoru z równaniem ruchu harmonicznego wynika zależność:

a = -ω²x

Poziom zaawansowany

Wyprowadzenie powyższych wzorów:

v=dx/dt=d[Acos(ωt+φ)]/dt=-Aωsin(ωt+φ),

bo pochodną funkcji cos(t) po czasie t jest funkcja -sin(t), zaś pochodną funkcji wewnętrznej ωt po czasie t jest ω.

a=dv/dt=d[-Aωsin(ωt+φ)]/dt=-Aω²cos(ωt+φ).

Ostatni wzór można zapisać jako:

a = -Aω²cos(ωt+φ) = -ω² · Acos(ωt+φ) = -ω²x