Funkcje trygonometryczne
W tym artykule odpowiadamy na pytanie, co to jest sinus, cosinus, tangens i cotangens kąta. Funkcje te definiujemy w różny sposób.
Funkcje trygonometryczne kąta ostrego
Niech dany będzie trójkąt prostokątny, zilustrowany poniższym rysunkiem:
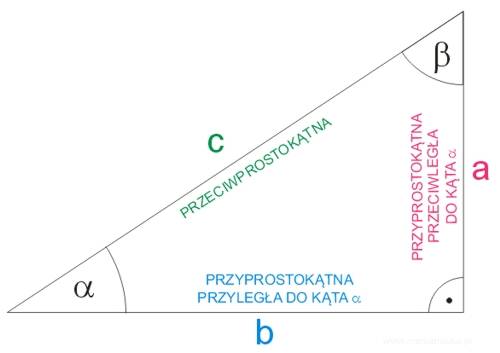
Określone są pewne związki trygonometryczne w trójkącie prostokątnym, a mianowicie definiujemy następujące funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym:
Sinus
Co to jest sinus? Oto definicja sinusa kąta ostrego.
Sinus kąta ostrego jest to stosunek przyprostokątnej przeciwległej kątowi ostremu \(\alpha\) do przeciwprostokątnej.
Zapiszemy teraz funkcję sinus dla kąta \(\beta\), używając powyższej definicji: \(\sin{\beta}=\frac{b}{c}\).
Cosinus
Cosinus kąta ostrego (czytaj: kosinus) jest to stosunek przyprostokątnej przyległej do kąta ostrego \(\alpha\) do przeciwprostokątnej.
Zapiszemy teraz funkcję cosinus dla kąta \(\beta\), używając powyższej definicji: \(\cos{\beta}=\frac{a}{c}\).
Tangens
Tangens kąta ostrego jest to stosunek przyprostokątnej przeciwległej kątowi ostremu \(\alpha\) do przyprostokątnej przyległej.
Zapiszemy teraz funkcję tangens dla kąta \(\beta\), używając powyższej definicji: \(tg{\beta}=\frac{b}{a}\). Czasem dla oznaczenia tangensa używa się skrótów: tan, tang.
Cotangens
Cotangens (czytaj kotangens) kąta ostrego jest to stosunek przyprostokątnej przyległej do kąta ostrego \(\alpha\) do przyprostokątnej przeciwległej.
Zapiszemy teraz funkcję cotangens dla kąta \(\beta\), używając powyższej definicji: \(ctg{\beta}=\frac{a}{b}\). Czasem dla oznaczenia cotangensa używa się skrótów: ctn, cot.
A oto rzadziej używane funkcje trygonometryczne kąta ostrego.
Secans
Secans (czytaj sekans) kąta ostrego jest to stosunek przeciwprostokątnej do przyprostokątnej przyległej kąta ostrego \(\alpha\).
Zapiszemy teraz funkcję secans dla kąta \(\beta\), używając powyższej definicji: \(sec{\beta}=\frac{c}{a}\).
Cosecans
Cosecans (czytaj kosekans) kąta ostrego jest to stosunek przeciwprostokątnej do przyprostokątnej przeciwległej kątowi ostremu \(\alpha\).
Zapiszemy teraz funkcję cosecans dla kąta \(\beta\), używając powyższej definicji: \(cosec{\beta}=\frac{c}{b}\). Czasem dla oznaczenia cotangensa używa się skrótu: csc.
Tabela wartości funkcji trygonometrycznych
Poniższa tabela przedstawia wartości funkcji trygonometrycznych dla często używanych miar kątów:
| \(\alpha\) | 0° | 30° | 45° | 60° | 90° |
| \(\sin{\alpha}\) | 0 | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| \(\cos{\alpha}\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | 0 |
| \(tg{\alpha}\) | 0 | \(\frac{\sqrt{3}}{3}\) | 1 | \(\sqrt{3}\) | - |
| \(ctg{\alpha}\) | - | \(\sqrt{3}\) | 1 | \(\frac{\sqrt{3}}{3}\) | 0 |
Tabela z funkcjami trygonometrycznymi jest tak często wykorzystywana w matematyce, że warto jej nauczyć się na pamięć. Najlepiej zrobić to za pomocą darmowej aplikacji, do której link znajduje się poniżej.
Zależności między funkcjami trygonometrycznymi kata ostrego
Zauważamy, że wprost z definicji można określić pewne zależności (czym jest odwrotność cotangensa, odwrotność cosinusa i sinusa):
\(ctg\alpha=\frac{1}{tg\alpha}\)
\( sec\alpha=\frac{1}{\cos{\alpha}}\)
\( cosec\alpha=\frac{1}{sin\alpha}\)
Zastosowanie funkcji trygonometrycznych
Głównym celem definiowania funkcji trygonometrycznych jest rozwiązywanie trójkątów, to znaczy wyznaczanie wszystkich jego boków i kątów. Poniżej prosty przykład zastosowania funkcji trygonometrycznej:
Przykład
Chłopiec stoi w odległości \(100\ m\) od latarni, którą widzi pod kątem 30°. Jaka jest wysokość latarni?
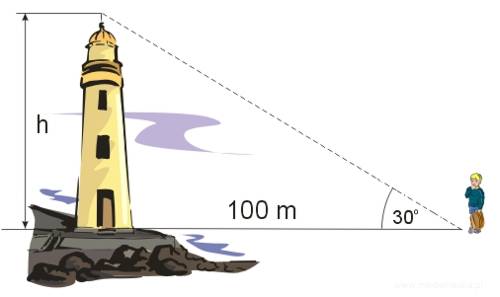
Korzystamy z definicji tangensa kąta ostrego:
\(tg{30^o}=\frac{h}{100\ m}/\cdot 100\ m\)
\(h=tg30^o\cdot 100\ m\)
\(h=\frac{\sqrt{3}}{3}\cdot 100\ m\)
\(h\approx 57,7\ m\)
To jedynie mały wycinek zastosowań funkcji trygonometrycznych. Funkcje te znajdują szerokie zastosowanie w fizyce i technice. Ruch harmoniczny, falowy, kołowy opisuje się z wykorzystaniem właśnie tych funkcji.
Funkcje trygonometryczne kąta skierowanego
W niniejszym artykule uogólnimy definicje funkcji trygonometrycznych kąta ostrego.
Niech dany będzie w układzie współrzędnych dowolny kąt skierowany o mierze \(\alpha\). Na końcowym ramieniu kąta obieramy dowolny punkt \(M\), dla którego określamy odciętą \(x\), rzędną \(y\) oraz promień wodzący \(r\) (patrz na poniższy rysunek):
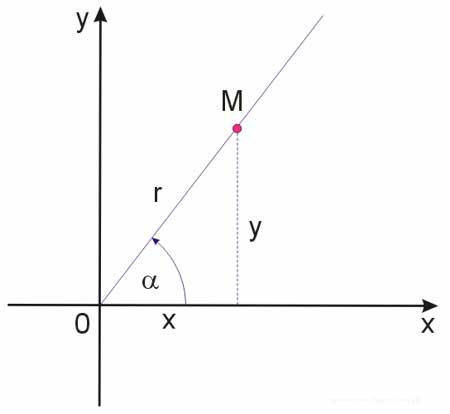
Definicja
\(\sin{\alpha}=\frac{rzędna}{promień} =\frac{y}{r}\)
\( \cos{\alpha}=\frac{odcięta}{promień} =\frac{x}{r}\)
\( tg{\alpha}=\frac{rzędna}{odcięta} =\frac{y}{x}\)
\( ctg{\alpha}=\frac{odcięta}{rzędna} =\frac{x}{y}\)
\( \sec{\alpha}=\frac{promień}{odcięta} =\frac{r}{x}\)
\( cosec{\alpha}=\frac{promień}{rzędna} =\frac{r}{y}\)
Zauważmy, że funkcje sinus i cosinus są określone dla każdego kąta (\(r\), które występuje w mianowniku, jest zawsze różne od zera). Funkcje tangens i cotangens nie są określone dla wszystkich kątów. Funkcja tangens nie jest określona dla kąta 90°, bo wówczas \(x=0\), a \(x\) jest w mianowniku.
Znak funkcji trygonometrycznych
Ponieważ r jest zawsze dodatnie, to:
- znak funkcji sinus zależy od znaku rzędnej,
- znak funkcji cosinus zależy od znaku odciętej,
- znak funkcji tangens i cotangens jest dodatni, gdy rzędna i odcięta są tego samego znaku.
Zapiszemy w tabeli znaki poszczególnych funkcji trygonometrycznych w kolejnych ćwiartkach układu współrzędnych:
| 0° | I ćwiartka | 90° | II ćwiartka | 180° | III ćwiartka | 270° | IV ćwiartka | 360° | |
| \(\sin{\alpha}\) | 0 | + | 1 | + | 0 | - | -1 | - | 0 |
| \(\cos{\alpha}\) | 1 | + | 0 | - | -1 | - | 0 | + | 1 |
| \(tg{\alpha}\) | 0 | + | x | - | 0 | + | x | - | 0 |
| \(ctg{\alpha}\) | x | + | 0 | - | x | + | 0 | - | x |
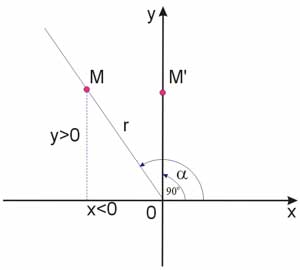
Objaśnienia do tabelki
Jak wypełnić samemu powyższą tabelkę? Weźmy na przykład kąt 90° i II ćwiartkę układu współrzędnych. Zaczynamy od kąta 90° (zobacz rysunek). Na ostatnim ramieniu kąta skierowanego o mierze 90° zaznaczono punkt \(M'\), którego rzędna jest równa \(y=r\), natomiast odcięta \(x=0\), więc:
\(\sin{90^o}=\frac{y}{r}=\frac{r}{r}=1\)
\(\cos{90^o}=\frac{x}{r}=\frac{0}{r}=0\)
\(tg{90^o}=\frac{y}{x}=\frac{y}{0}\) — funkcja nie jest określona
\(ctg{90^o}=\frac{x}{y}=\frac{0}{y}=0\)
Tak wyznaczone wartości zostały wpisane w kolumnę tabelki dla kąta 90°.
Teraz wyznaczymy znaki funkcji trygonometrycznych w II ćwiartce. Na końcowym ramieniu kąta o mierze α zaznaczono punkt \(M\), dla którego określamy \(x, y, r\). Widać, że \(x<0, y>0, r>0\), więc:
\(\sin{\alpha}=\frac{y}{r}>0\)
\(\cos{\alpha}=\frac{x}{r}<0\)
\(tg{\alpha}=\frac{y}{x}<0\)
\(ctg{\alpha}=\frac{x}{y}<0\)
Tak wyznaczone znaki wpisujemy do tabelki.
Funkcje trygonometryczne zmiennej rzeczywistej
Funkcje zmiennej rzeczywistej nazywamy funkcje, w których wartości argumentu i wartości funkcji należą do zbioru liczb rzeczywistych, niestety funkcje trygonometryczne kąta ostrego oraz funkcje trygonometryczne kąta skierowanego nie spełniają tego warunku, ponieważ argumentami tych funkcji są kąty (ich miary). Inaczej jest w przypadku miary łukowej kąta, która jest liczbą rzeczywistą. Funkcje trygonometryczne miary łukowej kąta są funkcjami zmiennej rzeczywistej. Definicja na przykład sinusa wygląda więc następująco:
Definicja
Sinus liczby \(x\) jest to sinus kąta skierowanego, którego miarą łukową jest liczba \(x\).
Podobnie definiujemy pozostałe funkcje trygonometryczne.
Zatem jeżeli mówimy „tangens liczby 5”, to w tym przypadku mamy na myśli tangens kąta skierowanego, którego miarą łukową tego kąta jest liczba 5.
Wszystkie własności funkcji trygonometrycznych kąta skierowanego są zachowane dla funkcji trygonometrycznych zmiennej rzeczywistej.
Zadania z rozwiązaniami

Zadanie nr 1.
Dany jest trójkąt równoramienny o podstawie długości \(a\), ramionach długości \(b\), kątami wewnętrznymi przy podstawie trójkąta \(\beta\) oraz \(\alpha\) przy wierzchołku trójkąta z którego opada wysokość \(h\) na podstawę trójkąta. Zapisać podstawowe funkcje trygonometryczne dla katów: \(\beta, \frac{\alpha}{2}\).

Zadanie nr 2.
Dany jest trójkąt prostokątny równoramienny o przyprostokątnej długości \(a=\sqrt{2}\). Oblicz długość podstawy korzystając z funkcji trygonometrycznych.

Zadanie nr 3.
Obliczyć długość podstawy prostokąta, jeżeli przekątna o długości \(d=2\sqrt{3}\) tworzy z podstawą kąt \(\alpha=30°\).

Zadanie nr 4.
Obliczyć promień \(R\) okręgu opisanego na sześciokącie foremnym, jeżeli wiadomo, że długość promienia wpisanego w ten wielokąt \(r=2\).

Zadanie nr 5 — maturalne.
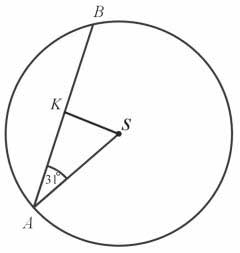 W okręgu o środku w punkcie \(S\) poprowadzono cięciwę \(AB\), która utworzyła z promieniem \(AS\) kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu \(S\) od cięciwy \(AB\) jest liczbą z przedziału
W okręgu o środku w punkcie \(S\) poprowadzono cięciwę \(AB\), która utworzyła z promieniem \(AS\) kąt o mierze 31° (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu \(S\) od cięciwy \(AB\) jest liczbą z przedziału
A. \(\langle \frac{9}{2};\frac{11}{2}\rangle\)
B. \(\langle \frac{11}{2};\frac{13}{2}\rangle\)
C. \(\langle \frac{13}{2};\frac{19}{2}\rangle\)
D. \(\langle \frac{19}{2};\frac{37}{2}\rangle\)

Zadanie nr 6 — maturalne.
Kąt \(\alpha\) jest ostry i \(tg{\alpha}=\frac{2}{3}\). Wtedy:
A. \(\sin{\alpha}=\frac{3\sqrt{13}}{26}\)
B. \(\sin{\alpha}=\frac{\sqrt{13}}{13}\)
C. \(\sin{\alpha}=\frac{2\sqrt{13}}{13}\)
D. \(\sin{\alpha}=\frac{3\sqrt{13}}{13}\)

Zadanie nr 7 — maturalne.
Kąt rozwarcia stożka ma miarę 120°, a tworzącą tego stożka ma długość 4. Objętość tego stożka jest równa
A. \(36\pi\)
B. \(18\pi\)
C. \(24\pi\)
D. \(8\pi\)

Zadanie nr 8 — maturalne.
Przekątna podstawy graniastosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
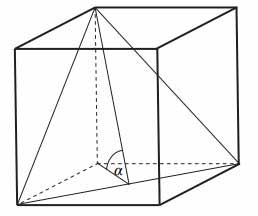
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt α o mierze
A. 30°
B. 45°
C. 60°
D. 75°

Zadanie nr 9 — maturalne.
Tangens kąta \(\alpha\) zaznaczonego na rysunku jest równy:
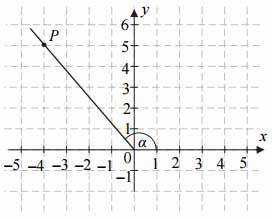
A. \(-\frac{\sqrt{3}}{3}\)
B. \(-\frac{4}{5}\)
C. \(-1\)
D. \(-\frac{5}{4}\)

Zadanie nr 10 — maturalne.
Przyprostokątna \(LM\) trójkąta prostokątnego \(KLM\) ma długość \(3\), a przeciwprostokątna \(KL\) ma długość \(8\) (zobacz rysunek).
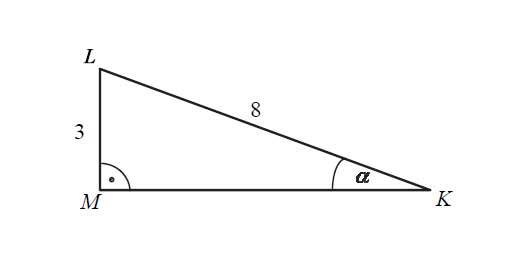
Wówczas miara α kąta ostrego LMK tego trójkąta spełnia warunek
- 27°<α≤30°
- 24°<α≤27°
- 21°<α≤24°
- 18°<α≤21°

Zadanie nr 11 — maturalne.
Sinus kąta ostrego \(\alpha\) jest równy \(\frac{4}{5}\). Wtedy
A. \(\cos{\alpha}=\frac{5}{6}\)
B. \(\cos{\alpha}=\frac{1}{5}\)
C. \(\cos{\alpha}=\frac{9}{25}\)
D. \(\cos{\alpha}=\frac{3}{5}\)

Zadanie nr 12 — maturalne.
Promień \(AS\) podstawy walca jest równy połowie wysokości \(OS\) tego walca. Sinus kąta \(OAS\) (zobacz rysunek) jest równy
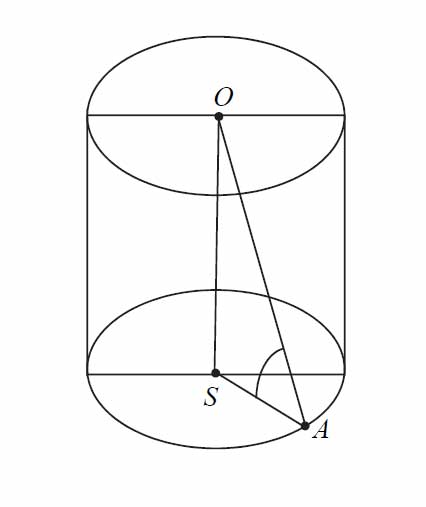
A. \(\frac{\sqrt{5}}{2}\)
B. \(\frac{2\sqrt{5}}{5}\)
C. \(\frac{1}{2}\)
D. \(1\)

Zadanie nr 13 — maturalne.
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha\) i \(\beta\) (zobacz rysunek).
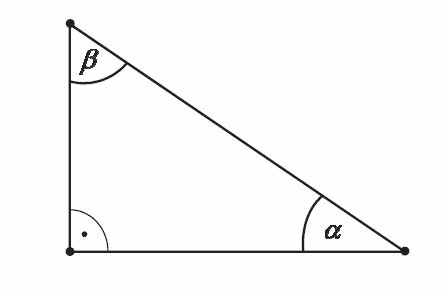
Wyrażenie \(2\cos{\alpha}−\sin{\beta}\) jest równe
A. \(2\sin{\beta}\)
B. \(\cos{\alpha}\)
C. \(0\)
D. \(2\)
Powiązane materiały
 Funkcje trygonometryczne
Funkcje trygonometryczne© medianauka.pl, 2011-03-22, A-1255
Data aktualizacji artykułu: 2023-07-20


 Sinus cosinus tangens cotangens 0 30 45 60 90 stopni
Sinus cosinus tangens cotangens 0 30 45 60 90 stopni Nauka wartości funkcji trygonometrycznych
Nauka wartości funkcji trygonometrycznych Wykres funkcji sinus
Wykres funkcji sinus Wykres funkcji cosinus
Wykres funkcji cosinus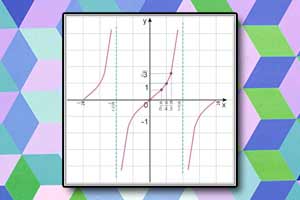 Wykres funkcji tangens
Wykres funkcji tangens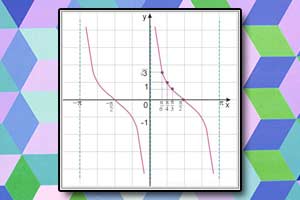 Wykres funkcji cotangens
Wykres funkcji cotangens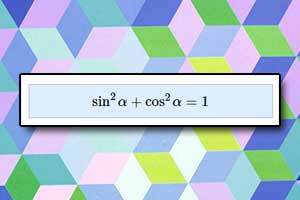 Wzory trygonometryczne, tożsamości trygonometryczne
Wzory trygonometryczne, tożsamości trygonometryczne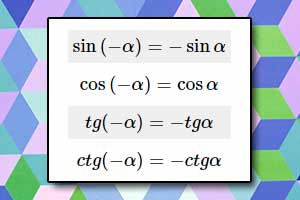 Wzory redukcyjne
Wzory redukcyjne Twierdzenie sinusów, cosinusów i tangensów
Twierdzenie sinusów, cosinusów i tangensów Funkcje cyklometryczne
Funkcje cyklometryczne