Rachunek prawdopodobieństwa
Rachunek prawdopodobieństwa albo inaczej probabilistyka to dział w matematyce, który zajmuje się modelowaniem zjawisk przypadkowych. Chodzi tu o takie zjawiska, czy zdarzenia, nazywane losowymi, których wyniku zakończenia nie da się w sposób jednoznaczny przedstawić. Będziemy się więc tutaj zajmować rzutami kostką, monetą, przewidywać występowanie konkretnych zdarzeń. Dział ten zajmuje się badaniem prawidłowości dotyczących możliwości uzyskania oczekiwanego wyniku zdarzeń losowych. Oczywiście powstanie tego działu matematyki było związane z hazardem i poznania szans na wygranie w konkretnej grze losowej. Najważniejszym chyba matematykiem, który zajmował się tą dziedziną matematyki, był J. Bernoulli. Dziś osiągnięcia tej dziedziny nauki wykorzystuje się w wielu innych dziedzinach, takich jak nauki przyrodnicze i techniczne. W tym miejscu należy też rozpatrywać elementy statystyki.
Kombinatoryka
To wstęp do rachunku prawdopodobieństwa. Ma także zastosowanie w informatyce, teorii liczb i grafów. Ta dziedzina matematyki, której podwaliny powstały już w starożytności, a rozwój przypada na XVI w., zajmuje się obliczaniem, ile jest zbiorów, które można utworzyć w zadany sposób z elementów danego skończonego zbioru elementów. Omówimy tutaj takie pojęcia jak: permutacja, kombinacja, wariacja.
TESTY I ZADANIA
Prawdopodobieństwo
Zajmujemy się w tym miejscu definiowaniem i obliczaniem prawdopodobieństwa.
TESTY I ZADANIA
Elementy statystyki opisowej
Definiujemy w tym miejscu podstawowe pojęcia statystyki, jakimi są: dominanta, średnia arytmetyczna, geometryczna, mediana, wariancja i odchylenie standardowe. Z reguły ten dział matematyki zajmuje się badaniem zjawisk, które występują masowo. Rachunek prawdopodobieństwa jest jednym z narzędzi badań w tym obszarze. Statystyka matematyczna zajmuje się statystyczną analizą danych oraz weryfikacją hipotez statystycznych za pomocą testów statystycznych.
TESTY I ZADANIA
© medianauka.pl, 2016-07-05, A-3198
Data aktualizacji artykułu: 2023-11-01

 Silnia
Silnia Symbol Newtona
Symbol Newtona Permutacja
Permutacja Kombinacja
Kombinacja Wariacje bez powtórzeń
Wariacje bez powtórzeń Wariacje z powtórzeniami
Wariacje z powtórzeniami Kombinatoryka
Kombinatoryka Doświadczenie i zdarzenie losowe
Doświadczenie i zdarzenie losowe Prawdopodobieństwo
Prawdopodobieństwo Prawdopodobieństwo warunkowe
Prawdopodobieństwo warunkowe Zdarzenia niezależne
Zdarzenia niezależne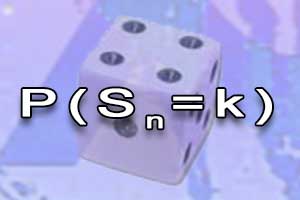 Schemat Bernoulliego
Schemat Bernoulliego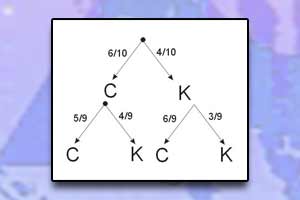 Drzewo prawdopodobieństwa
Drzewo prawdopodobieństwa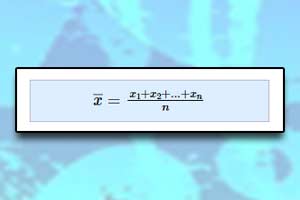 Średnia arytmetyczna
Średnia arytmetyczna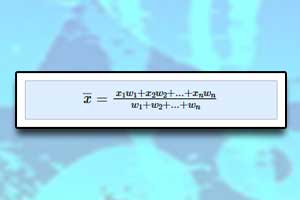 Średnia ważona
Średnia ważona Mediana
Mediana Dominanta
Dominanta Wariancja i odchylenie standardowe
Wariancja i odchylenie standardowe