Zdarzenia niezależne

Definicja

Zdarzenia losowe A i B nazywamy niezależnymi, gdy prawdopodobieństwo iloczynu tych zdarzeń jest równe iloczynowi ich prawdopodobieństw. W przeciwnym przypadku zdarzenia te nazywamy zależnymi.

$P(A\cap B)=P(A)P(B)$

Przykład

Rzucamy dwukrotnie monetą. Sprawdzić, czy zdarzenie A, polegające na wyrzuceniu w pierwszym rzucie reszki i B - wyrzucenie orła w drugim rzucie są niezależne.

$P(A)=\frac{1}{2}\\ P(B)=\frac{1}{2}\\ P(A\cap B)=\frac{1}{4}\\ P(A\cap B)=P(A)P(B)$

Zdarzenia są niezależne.

Jeszcze małe uzupełnienie. Dlaczego prawdopodobieństwo iloczynu jest równe jednej czwartej? Skoro rzucamy monetą dwa razy, to mamy czteroelementowy zbiór zdarzeń elementarnych: {(o,o),(r,r),(o,r),(r,o)}, a zdarzeniu będącym iloczynem zdarzeń A i B sprzyja tylko jeden wynik: (r,o).

Niezależność trzech zdarzeń

Definicja

Zdarzenia losowe A, B i C nazywamy niezależnymi, gdy zachodzą równości:

$P(A\cap B)=P(A)P(B)\\ P(A\cap C)=P(A)P(C)\\ P(B\cap C)=P(B)P(C)\\ P(A\cap B\cap C)=P(A)P(B)P(C)$

W sposób analogiczny definiujemy niezależność dowolnej liczby zdarzeń.

Inne zagadnienia z tej lekcji

Doświadczenie i zdarzenie losowe

Co to jest doświadczenie losowe i zdarzenie losowe i zdarzenia elementarne?

Własności prawdopodobieństwa

Podstawowe twierdzenia o prawdopodobieństwach zdarzeń wraz z przykładami ich stosowania.

Zastosowanie kombinatoryki do prawdopodobieństwa

Przykłady z rachunku prawdopodobieństwa z wykorzystania elementów kombinatoryki.

Prawdopodobieństwo warunkowe i całkowite

Definicja prawdopodobieństwa warunkowego i twierdzenie o prawdopodobieństwie zupełnym.

Schemat Bernoulliego

Obliczanie prawdopodobieństwa w oparciu o schemat Bernoulliego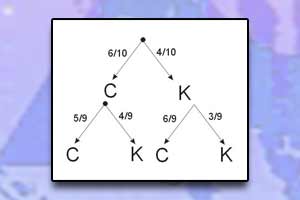

Drzewo prawdopodobieństwa (stochastyczne)

Kiedy przy obliczaniu prawdopodobieństwa można posłużyć się grafem, tak zwanym drzewem stochastycznym.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.