Funkcje
Funkcja albo inaczej odwzorowanie, przekształcenie jest to pewne przyporządkowanie określone na elementach dwóch zbiorów X i Y, zgodnie z którym każdemu elementowi x ze zbioru X odpowiada dokładnie jeden element y ze zbioru Y. Funkcja posiada wiele ciekawych właściwości, rozróżniamy wiele typów funkcji. Zastosowanie tego pojęcia w matematyce oraz naukach przyrodniczych i technicznych jest nie do przecenienia.
Spis treści
Funkcja i jej własności
Omawiamy w tym miejscu definicję pojęcia funkcji oraz omawiamy podstawowe jej cechy. Jest to podstawa wiedzy o funkcjach, którą należy przyswoić przed przystąpieniem do studiowania tematów dotyczących różnych typów funkcji, które omawiamy dalej.
TESTY I ZADANIA
Funkcja liniowa
Funkcja liniowa jest to funkcja w postaci f(x)=ax+b. Jest to najprostszy rodzaj odwzorowania. Szczególnym przypadkiem funkcji liniowej jest proporcjonalność prosta.
TESTY I ZADANIA
Funkcja kwadratowa
Funkcja to jest to funkcja w postaci f(x)=ax2+bx+c, przy czym a jest różne od zera. Funkcja ta ma ogromne zastosowania praktyczne.
TESTY I ZADANIA
Wielomiany
W tym rozdziale wprowadzamy pojęcie wielomianu, badamy jego właściwości wraz z omówieniem metod znajdowania pierwiastków wielomianu. Zajmujemy się tu także działaniami na wielomianach.
TESTY I ZADANIA
Inne funkcje
W tym rozdziale gromadzimy wiedzę na temat wszystkich pozostałych typów funkcji, które nie zostały wymienione wyżej, w tym funkcji potęgowej, wykładniczej, wymiernej, logarytmicznej i trygonometrycznej.
TESTY I ZADANIA
© medianauka.pl, 2016-07-09, A-3202
Data aktualizacji artykułu: 2023-01-30

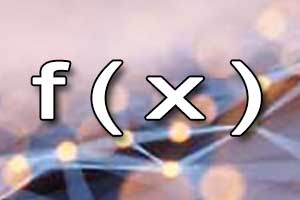 Funkcja
Funkcja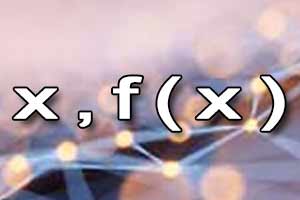 Wyznaczanie wartości i argumentów funkcji
Wyznaczanie wartości i argumentów funkcji Wyznaczanie dziedziny funkcji
Wyznaczanie dziedziny funkcji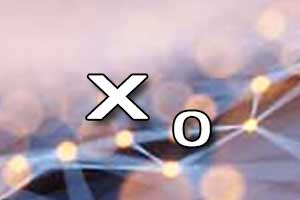 Miejsce zerowe funkcji
Miejsce zerowe funkcji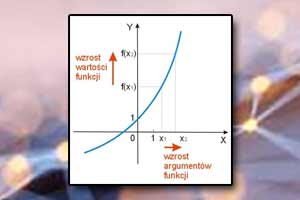 Monotoniczność funkcji
Monotoniczność funkcji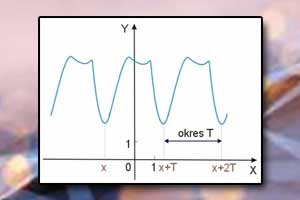 Okres funkcji
Okres funkcji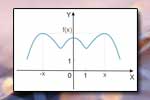 Parzystość funkcji
Parzystość funkcji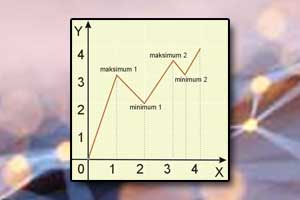 Ekstremum funkcji
Ekstremum funkcji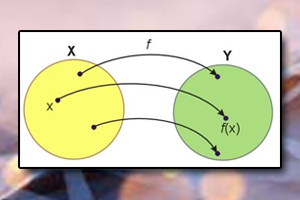 Funkcja różnowartościowa
Funkcja różnowartościowa Układ współrzędnych
Układ współrzędnych Wykres funkcji
Wykres funkcji Funkcja odwrotna
Funkcja odwrotna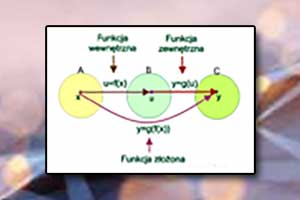 Funkcja złożona
Funkcja złożona Przesunięcie wykresu funkcji
Przesunięcie wykresu funkcji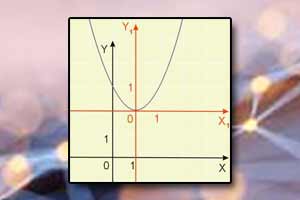 Pomocniczy układ współrzędnych
Pomocniczy układ współrzędnych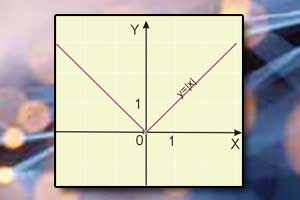 Wykres funkcji z wartością bezwzględną
Wykres funkcji z wartością bezwzględną Funkcja liniowa
Funkcja liniowa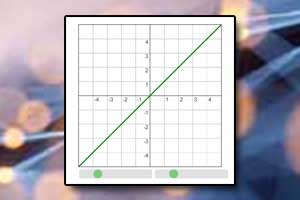 Wykres funkcji liniowej
Wykres funkcji liniowej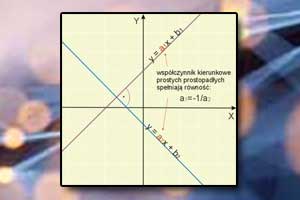 Wzajemne położenie prostych na płaszczyźnie
Wzajemne położenie prostych na płaszczyźnie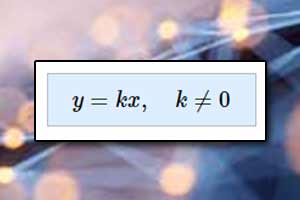 Proporcjonalność prosta
Proporcjonalność prosta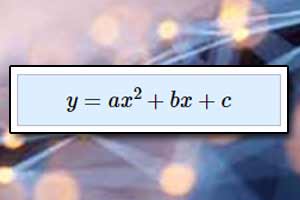 Funkcja kwadratowa
Funkcja kwadratowa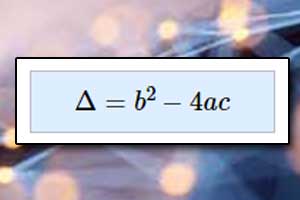 Postać kanoniczna trójmianu kwadratowego
Postać kanoniczna trójmianu kwadratowego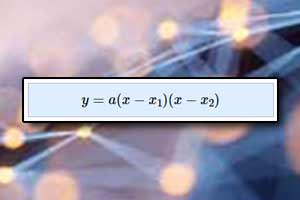 Postać iloczynowa trójmianu kwadratowego
Postać iloczynowa trójmianu kwadratowego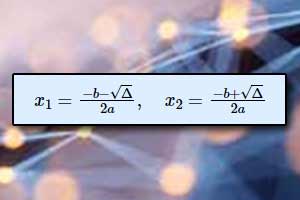 Miejsca zerowe funkcji kwadratowej
Miejsca zerowe funkcji kwadratowej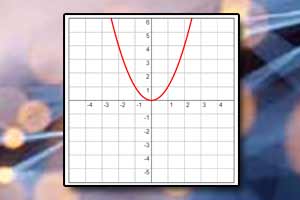 Wykres funkcji kwadratowej
Wykres funkcji kwadratowej Wielomian
Wielomian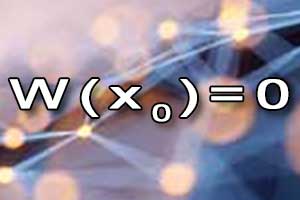 Pierwiastek, miejsce zerowe wielomianu
Pierwiastek, miejsce zerowe wielomianu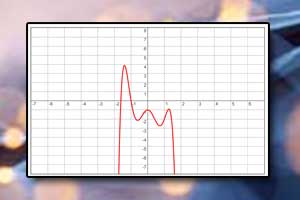 Wykres wielomianu
Wykres wielomianu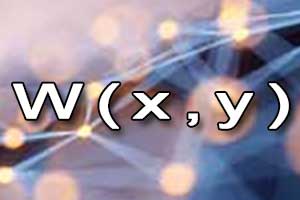 Wielomian dwóch zmiennych
Wielomian dwóch zmiennych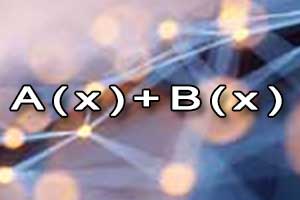 Dodawanie i odejmowanie wielomianów
Dodawanie i odejmowanie wielomianów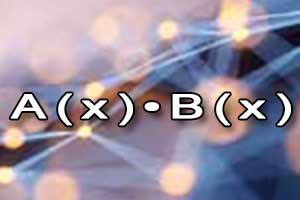 Mnożenie wielomianów
Mnożenie wielomianów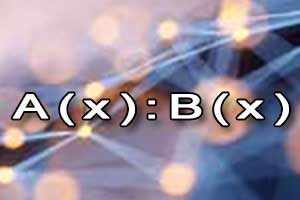 Dzielenie wielomianów
Dzielenie wielomianów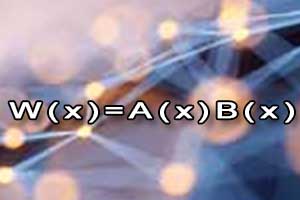 Rozkład wielomianu na czynniki
Rozkład wielomianu na czynniki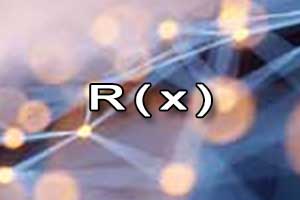 Schemat Hornera
Schemat Hornera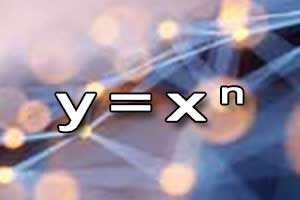 Funkcja potęgowa
Funkcja potęgowa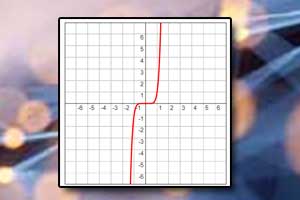 Wykres funkcji potęgowej
Wykres funkcji potęgowej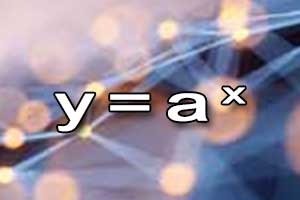 Funkcja wykładnicza
Funkcja wykładnicza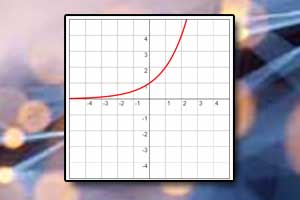 Wykres funkcji wykładniczej
Wykres funkcji wykładniczej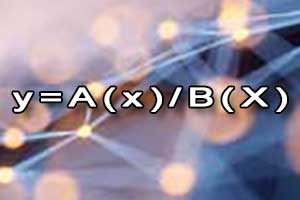 Funkcja wymierna
Funkcja wymierna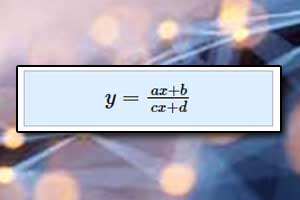 Funkcja homograficzna
Funkcja homograficzna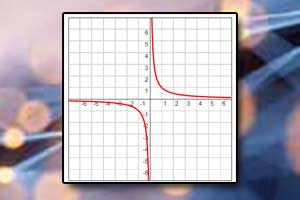 Wykres funkcji homograficznej
Wykres funkcji homograficznej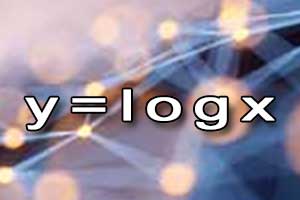 Funkcja logarytmiczna
Funkcja logarytmiczna Funkcje trygonometryczne
Funkcje trygonometryczne Funkcja wektorowa
Funkcja wektorowa