Miejsce zerowe funkcji

Co to jest miejsce zerowe funkcji?

Definicja

Miejsce zerowe funkcji jest to taka wartość argumentu, dla której wartość funkcji jest równa zeru.

Powyższa funkcja oznacza, że wzór na miejsce zerowe funkcji \(f(x)\) możemy zapisać następująco:

\(f(x)=0\)

Punkt zerowy najczęściej oznaczamy przez \(x_0\). Jeśli funkcja posiada więcej miejsc zerowych niż jedno, to oznaczamy je przez \(x_1, x_2,...\) itd.

Jak obliczyć miejsce zerowe funkcji?

Aby znaleźć miejsca zerowe funkcji musimy rozwiązać równanie \(f(x)=0\). Obliczanie miejsca zerowego sprowadza się zatem do rozwiązania odpowiedniego równania.

Przykłady

Dana jest funkcja \(f(x)=4-x\). Aby znaleźć jej miejsca zerowe rozwiązujemy więc równanie:

\(0=4-x\)

\(x=4\)

Zatem funkcja ta ma jedno miejsce zerowe \(x_0=4\).

Miejsce zerowe funkcji ściśle związane jest z miejscem przecięcia się wykresu funkcji z osią OX, a mianowicie zakładając, że miejscem zerowym funkcji \(f(x)\) jest \(x_0\), to punkt przecięcia się wykresu z osią \(OX\) ma współrzędne \((x_0 ,0)\).

Dla powyższego przykładu miejscem przecięcia się wykresu funkcji z osią \(OX\) jest punkt \((4,0)\).

Przykłady

Zbadajmy ile i jakie miejsca zerowe posiada funkcja \(y=-x^2+1\) i spróbujmy to zrobić bez znajomości rozwiązywania równań kwadratowych.

Sporządzimy tabelkę zmienności funkcji i sporządzimy szkic wykresu tej funkcji.

\(x\)	0	1	-1	2	-2
\(y\)	1	0	0	-3	-3

Sporządzamy szkic wykresu funkcji i zaznaczamy miejsca zerowe.

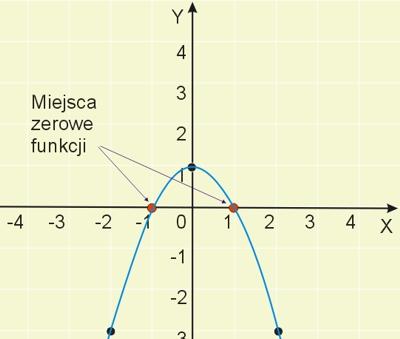
miejsca zerowe funkcji

Widzimy, że funkcja ma 2 miejsca zerowe, a z tabelki możemy odczytać, że są to \(x_1=-1\) i \(x_2=1\).

Pytania

Jak obliczyć miejsce zerowe funkcji kwadratowej?

Tak jak dla każdego przypadku funkcji, należy rozwiązać równanie \(f(x)=0\). W tym przypadku otrzymamy równanie kwadratowe. Więcej na temat miejsc zerowych funkcji kwadratowej znajdziesz tutaj.

Funkcja kwadratowa \(y=ax^2+bx+c\) ma miejsca zerowe w przypadku, gdy \(\Delta\geq{0}\). Są to:

\(x_1=\frac{-b-\sqrt{\Delta}}{2a}\)

\({x_2=\frac{-b+\sqrt{\Delta}}{2a}}\)

Przypomnijmy, że \(\Delta=b^2-4ac\) to wyróżnik trójmianu kwadratowego.

W szczególnym przypadku, gdy \(\Delta=0\) oba pierwiastki są sobie równe (\(x_1=x_2=\frac{-b}{2a}=x_0\)).

Jak obliczyć miejsce zerowe funkcji liniowej?

Funkcja liniowa dana jest wzorem \(f(x)=ax+b\). Rozwiązując równanie \(f(x)=0\), czyli:

\](ax+b=0\)

\( ax=-b/:a, a\neq 0\)

Otrzymaliśmy wzór na miejsce zerowe funkcji liniowej.

\( x=-\frac{b}{a}\)

Dla przykładu miejscem zerowym funkcji \(y=3x+2\) jest to \(x_0=-\frac{2}{3}\).

Kiedy funkcja nie ma miejsc zerowych?

Funkcja \(f(x)\) nie ma miejsc zerowych, jeżeli nie ma takich argumentów, dla których \(f(x)=0\). Mówiąc inaczej, jeżeli wykres danej funkcji nie przecina w żadnym punkcie osi OX, to funkcja ta nie posiada miejsc zerowych.