Ekstremum funkcji

Ekstremum funkcji nazywamy minimum funkcji lub maksimum funkcji. Poniżej zdefiniowano oba pojęcia na podstawie założenia: \(x_0\in (a,b)\) i funkcja \(f\) jest określona w tym przedziale.

Maksimum funkcji

Funkcja \(f\) osiąga w punkcie \(x_0\) maksimum, jeżeli istnieje taki przedział \((m,n)\subset(a,b)\) o środku w punkcie \(x_0\), w którym dla każdego \(x\in (m,n)\) różnego od \(x_0\) spełniona jest nierówność \(f(x)<f(x_0)\).

Przykłady

Rysunek ilustruje wykres funkcji \(f(x)=-x^2+1\).

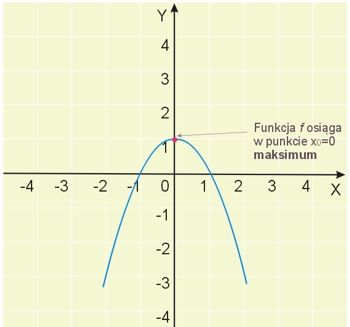
Widzimy, że funkcja ma jedno maksimum w punkcie \(x_0=0\) równe 1.

Przedział \((m,n)\), o którym mowa w definicji, to może być dla przykładu przedział \((-1,1)\), albo \((-100,100)\) lub \((-5,5)\). Widzimy, że dla dowolnej liczby różnej od \(x_0\) z tych przykładowych przedziałów wszystkie wartości funkcji są mniejsze od maksimum, czyli wartości funkcji w punkcie \(x_0=0\).

Minimum funkcji

Funkcja \(f\) osiąga w punkcie \(x_0\) minimum, jeżeli istnieje taki przedział \((m,n)\subset(a,b)\) o środku w punkcie \(x_0\), w którym dla każdego \(x\in (m,n)\) różnego od \(x_0\) spełniona jest nierówność \(f(x)>f(x_0)\).

Przykłady

Rysunek ilustruje wykres funkcji \(f(x)=x^2+1\).

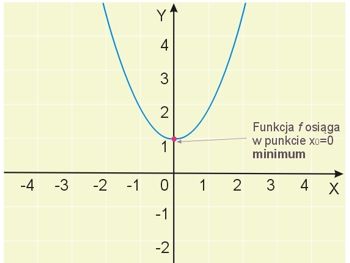
Widzimy, że funkcja ma jedno minimum w punkcie \(x_0=0\) równe 1.

Przedział \((m,n)\), o którym mowa w definicji to może być dla przykładu przedział (-1,1), albo (-100,100) lub (-5,5). Widzimy, że dla dowolnej liczby różnej od \(x_0=0\) z tych przykładowych przedziałów wszystkie wartości funkcji są większe od minimum, czyli wartości funkcji w punkcie \(x_0=0\).

Minimum lokalne i maksimum lokalne

Minimum i maksimum są pojęciami lokalnymi, to znaczy, że obowiązują jedynie w pewnym przedziale. Funkcja może mieć kilka minimum i kilka maksimum jednocześnie. Zdarza się też, że minimum może być większe niż maksimum. Przyjrzyjmy się poniższej ilustracji, na której wykreślono funkcję określoną w przedziale \(\langle 0,4 \rangle\).

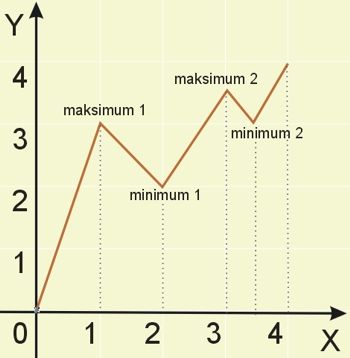
Mamy tutaj dwa maksima i dwa minima. Widać, że minimum 2 jest takie samo jak maksimum 1 (minimum wcale nie musi być mniejsze od maksimum). Ponadto minimum wcale nie oznacza najmniejszej wartości funkcji (tutaj równej 0), a maksimum nie musi być równe największej wartości funkcji, która w tym przypadku wynosi 4.

Dlaczego w punkcie \(x=4\) nie mamy maksimum, a w punkcie \(x=0\) nie mamy minimum? Dlatego, że nie możemy określić przedziału \((m,n)\), o którym mowa w definicji, a którego punkty 0 i 4 byłyby środkiem. Są to w tym przypadku najmniejsze i największe wartości funkcji.

Pytania

Jak obliczyć ekstremum funkcji?

Ekstrema funkcji najczęściej znajduje się , wykorzystując własności pochodnej funkcji. Wyznaczanie ekstremum funkcji zostało omówione w artykule Pochodna a ekstremum funkcji. Odnośnik do tego artykułu znajdziesz też poniżej.

Czym różnią się pojęcia ekstremum lokalne od ekstremum globalnego?

Ekstremum lokalne (czyli minimum lokalne lub maksimum lokalne) dotyczy pewnego otoczenia punktu (przedziału otwartego), w którym funkcja w żadnym punkcie nie przyjmuje wartości większych (maksimum) lub mniejszych (minimum). Ekstremum globalne to największa lub najmniejsza wartość funkcji w całej jej dziedzinie.

Powiązane materiały

Pochodna funkcji a ekstremum

Miejsce zerowe funkcji

Monotoniczność funkcji

Funkcja okresowa

Parzystość funkcji

Funkcja różnowartościowa

Własności funkcji