Przedziały liczbowe

W matematyce często stosujemy tak zwane przedziały liczbowe. Określają one zakres liczb. Jest to bardzo wygodny sposób zapisu podzbioru zbioru liczb rzeczywistych.

Przedział liczbowy jest to zbiór liczb rzeczywistych zawartych pomiędzy liczbami \(a\) i \(b\), przy czym \(a<b\), albo zbiór liczb rzeczywistych większych lub mniejszych od ustalonej liczby \(a\).

Jeżeli interesuje nas zakres liczb od 0 do 1 włącznie, możemy to zapisać za pomocą przedziału domkniętego \(⟨0;1⟩\) lub \([0,1]\). Jeżeli chcielibyśmy zapisać zbiór liczb większych od 0 i mniejszych od 1 możemy użyć przedziału otwartego \((0;1)\). A oto bardziej ścisłe określenie pojęcia przedziałów.

Definicje przedziałów

Nazwa przedziału	Oznaczenie	Definicja
przedział (obustronnie) otwarty	\((a;b)\)	\(x\in(a;b) \Leftrightarrow a<x<b\)
przedział (obustronnie) zamknięty (domknięty)	\(⟨a;b⟩\) lub \([a,b]\)	\(x\in ⟨a;b⟩ \Leftrightarrow a\leq x\leq b\)
przedział lewostronnie zamknięty (domknięty)	\(⟨a;b)\) lub \([a,b)\)	\(x\in ⟨a;b) \Leftrightarrow a\leq x<b\)
przedział prawostronnie zamknięty (domknięty)	\((a;b⟩\) lub \((a,b]\)	\(x\in(a;b⟩ \Leftrightarrow a<x\leq b\)
przedziały nieograniczone (nieskończone)	\((-\infty;a)\) \( (a;\infty)\)	\(x\in(-\infty;a) \Leftrightarrow x<a\) \( x\in(a;∞)\Leftrightarrow x>a\)

Przedziały na osi liczbowej

Przedziały mają swoją interpretację geometryczną. Poniższy rysunek ilustruje przedział domknięty \(\langle a;b\rangle \) i otwarty \((a;b)\):

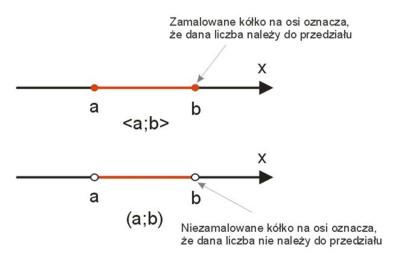
interpretacja geometryczna przedziałów

Poniżej znajduje się interpretacja geometryczna przedziałów jednostronnie domkniętych.

interpretacja geometryczna przedziałów jednostronnie domknietych

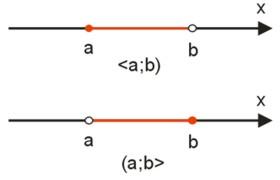
Powyższy sposób graficznego przedstawiania przedziałów jest dobry, ale stwarza trudności podczas zaznaczania na osi wielu różnych przedziałów liczbowych. Stosujemy wówczas nieco inną, bardziej praktyczną metodę (jak na poniższym rysunku).

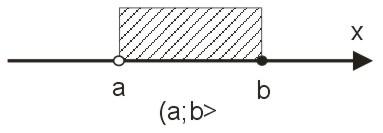
interpretacja geometryczna przedziałów

Na poniższym rysunku zilustrowano dwa przedziały liczbowe na jednej osi. Poprzez kreskowanie pól możemy łatwo wyznaczyć na przykład iloczyn (część wspólną) dwóch przedziałów. W poniższym przykładzie od razu widać, że częścią wspólną przedziałów \((a;b\rangle \) i \((c;d)\) jest przedział \((c;b\rangle \).

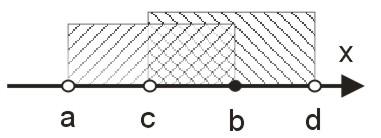
Iloczyn przedziałów liczbowych

Działania na przedziałach liczbowych

Pamiętajmy, że przedziały to zbiory liczb, więc stosujemy tutaj zasady działań na zbiorach (przypomnij sobie informacje na temat: sumy, różnicy oraz iloczynu zbiorów). Szczególnie często będziesz korzystał z sumy i iloczynu przedziałów liczbowych przy okazji rozwiązywania układów równań i nierówności. Poniżej zamieszczono kilka przykładów działań na przedziałach.

Przykład 1

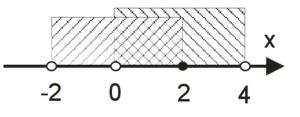
przedziały liczbowe

Suma przedziałów: \((-2;2\rangle \cup (0;4) = (-2;4)\)

Iloczyn przedziałów: \((-2;2\rangle \cap (0;4) = (0;2\rangle \)

Różnica przedziałów:

\((-2;2\rangle \setminus (0;4) = (-2;0\rangle \)

Zero należy do przedziału \((-2;2\rangle \), ale nie należy do przedziału \((0;4)\), więc należy do różnicy tych przedziałów w myśl definicji, że element należy do różnicy zbiorów, jeżeli należy do pierwszego zbioru i nie należy do zbioru drugiego.

\((0;4)\setminus (-2;2\rangle = (2;4)\)

Liczba 2 należy do przedziału \((-2;2\rangle\), a więc nie może należeć do rozpatrywanej różnicy przedziałów
W przypadku wyznaczania różnicy przedziałów zmienia się w niektórych przypadkach rodzaj przedziału z domkniętego na otwarty i odwrotnie.

Przykład 2

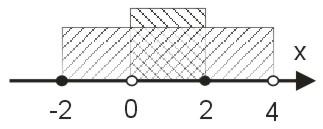
Przedziały liczbowe

Suma przedziałów:

\(\langle -2;4)\cup (0;2\rangle = \langle -2;4)\)

Iloczyn przedziałów:

\(\langle -2;4)\cap (0;2\rangle = (0;2\rangle\)

Różnica przedziałów:

\(\langle -2;4)\setminus (0;2\rangle = \langle-2;0\rangle \cup (2;4)\)

\((0;2\rangle \setminus \langle -2;4) = \emptyset \)

Przykład 3

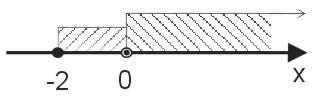
Przedziały liczbowe

Suma przedziałów:

\(\langle -2;0)\cup \langle 0;\infty) = \langle -2;\infty )\)

Iloczyn przedziałów:

\(\langle -2;0) \cap \langle 0;\infty) = \emptyset\)

Różnica przedziałów:

\(\langle -2;0)\setminus \langle 0;\infty) = \langle -2;0)\)

\(\langle 0;\infty)\setminus \langle -2;0) = \langle 0;\infty)\)

Zadania z rozwiązaniami

Zadanie nr 1.

Zaznacz na osi liczbowej przedziały (-5; -2⟩ ∪ (-1; 5⟩ oraz ⟨-6; -3) ∪ ⟨0; 1⟩. Zaznacz na osi część wspólną tych zbiorów oraz zapisz wynik za pomocą przedziału liczbowego.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Znaleźć sumę, iloczyn oraz różnicę zbiorów \([-3; 3)\) i \((-4; 2]\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Znaleźć sumę, iloczyn oraz różnicę zbiorów \((-1; 1)\) i \(\langle2; 3)\).

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Zapisać za pomocą przedziału liczbowego zbiór wszystkich wartości x, które spełniają układ:

\(\begin{cases}x\geq -1\\ x>-2 \\ x<3 \end{cases}\)

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności \(-4\leq x-1\leq 4\).

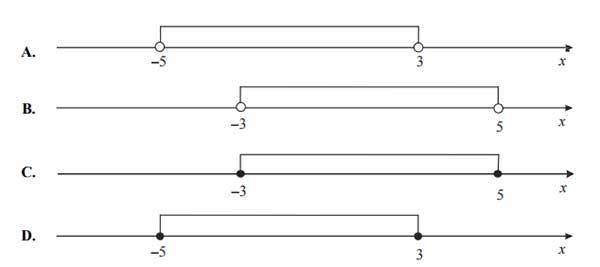
rysunek

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Rozważamy przedziały liczbowe \((−\infty, 5)\) i \(\langle −1, +\infty)\). Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?

A. \(6\)

B. \(5\)

C. \(4\)

D. \(7\)

Pokaż rozwiązanie zadania.