Liczby wymierne
Co to jest liczba wymierna?
Dawniej zbiór liczb wymiernych oznaczano literą \(\mathbb{W}\).
Przykłady liczb wymiernych
- Liczbami wymiernymi są na przykład: \(\frac{1}{2}\), \(\frac{6}{3}\) (czyli 2), \(\frac{0}{7}\) (czyli 0), \(-\frac{5}{10}\) (czyli \(-\frac{1}{2}\)), 0,01 (czyli \(\frac{1}{100}\)), \(\frac{3}{2}\) itd.
- Mimo że liczby 5, -2 i 0,3333... nie są wyrażone w postaci ułamka\(\frac{a}{b}\), to są liczbami wymiernymi, ponieważ można je wyrazić w takiej postaci: \(5=\frac{5}{1}\),\(0,3333...=\frac{1}{3}\), \(-2=\frac{-4}{2}\)
Własności zbioru liczb wymiernych
Zbiór liczb wymiernych jest zbiorem nieskończonym, ponadto nie ma w nim liczby najmniejszej, ani największej.
Zbiór liczb wymiernych jest przeliczalny i uporządkowany.
Między dwoma liczbami wymiernymi istnieje zawsze taka liczba wymierna, która jest większa od pierwszej i mniejsza od drugiej.
Podzbiorem zbioru liczb wymiernych jest zbiór liczb całkowitych, \(\mathbb{Z} \subset \mathbb{Q}\).
Ułamki zwykłe
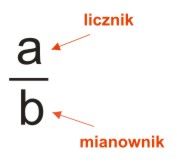
Iloraz \(\frac{a}{b}\) nazywamy ułamkiem zwykłym właściwym, jeżeli \(a<b\) oraz niewłaściwym, jeżeli \(a\geq b\). Liczbę a nazywamy licznikiem, a liczbę b — mianownikiem ułamka.
Przykład
- \(\frac{1}{2}\), \(\frac{5}{8}\), \(\frac{100}{101}\) to ułamki zwykłe właściwe;
- \(\frac{2}{1}\), \(\frac{8}{5}\), \(\frac{101}{100}\) to ułamki zwykłe niewłaściwe.
Ułamki dziesiętne
Ułamki o mianownikach 10, 100, 1000, 10000 itd. możemy zapisać w dziesiątkowym systemie pozycyjnym, oddzielając przecinkiem (lub kropką) część całkowitą i dziesiąte, setne, tysięczne itd. części tej liczby.
Przykład
Oto przykłady ułamków dziesiętnych:
- 2/10 = 0,2
- 14/100 = 0,14
- 2/1000 = 0,002
- 111/100 = 1,11
Aby zamienić ułamek zwykły na ułamek dziesiętny, należy wykonać dzielenie pisemne licznika przez mianownik. W wyniku dzielenia możemy uzyskać ułamek dziesiętny skończony lub ułamek dziesiętny nieskończony okresowy.
Każda liczba wymierna ma dokładnie jedno rozwinięcie dziesiętne: okresowe lub skończone.
Przykłady
- \(\frac{5}{4}=1.25\) — jest to przykład ułamka dziesiętnego skończonego.
- \(\frac{1}{3}=0.333...=0.(3)\) — jest to przykład ułamka dziesiętnego nieskończonego okresowego. Ponieważ po kropce liczba „3” powtarza się nieskończenie wiele razy, używamy zapisu polegającego na ujęciu okresu w nawiasach okrągłych.
Gdy zechcemy zamienić ułamek zwykły na dziesiętny, to jest to proste, jeżeli mamy do czynienia z ułamkiem dziesiętnym skończonym (np. 0,11 = 11/100), natomiast w przypadku ułamka okresowego trzeba stosować metody, które zostaną omówione w dalszej części kursu.
Działania na liczbach wymiernych
W zbiorze liczb wymiernych wykonywalne są następujące działania:
- dodawanie;
- odejmowanie;
- mnożenie;
- dzielenie.
Ciekawostki
Która z liczb: 1 czy 0,999... jest większa?
Aby to sprawdzić, zamieńmy ułamek okresowy \(0,(9)\) na ułamek zwykły. Niech \(x=0,999...\). Obie strony tego równania mnożymy przez 10 i otrzymujemy \(10x=9,999...\). Mamy zatem prosty układ równań:
\(\begin{cases}10x= 9,999...\\ x=0,999...\end{cases}\).
Kiedy odejmiemy od pierwszego równania drugie, otrzymamy:
\(9x=9,000...\)
\(9x=9/:9\)
\(x=1\)
Przecież na początku zapisaliśmy, że \(x=0,999...\)! Wnioskujemy więc, że liczby te są ... równe!
Oczywiście nie mamy tutaj do czynienia z żadnym przybliżeniem.
Każdy ułamek dziesiętny, mający okres 9 można zastąpić ułamkiem dziesiętnym skończonym.
A więc dla przykładu:
- 0,8(9) = 0,9
- 1,999... = 2
- 0,1(9) = 0,2
1 i 0,999... to po prostu różny sposób zapisu tej samej liczby.
Pytania
Czy 0 jest liczbą wymierną?
Tak, ponieważ da się je wyrazić w postaci ułamka, na przykład \(\frac{0}{1}\).
Jak sprawdzić, czy liczba jest wymierna?
Liczba jest wymierna, jeżeli jest:
- liczbą całkowitą,
- ułamkiem zwykłym,
- liczbą mieszaną,
- ułamkiem dziesiętnym o skończonej liczbie cyfr,
- ułamkiem dziesiętnym o rozwinięciu nieskończonym, ale okresowym, począwszy od określonej pozycji cyfry.
Jeżeli liczba jest zapisana w inny sposób, to należy stosować różne metody. Nie ma jednego algorytmu na sprawdzenie, czy dana liczba jest wymierna, czy niewymierna. Najczęściej stosuje się dowód nie wprost, czyli założenie, że dana liczba jest wymierna, czyli że da się wyrazić w postaci ilorazu dwóch liczb całkowitych \(\frac{p}{q}\), przy czym q jest różne od zera i poprzez dochodzenie do sprzeczności można wykazać, że dana liczba nie jest wymierna.
Dla pierwiastków można zastosować następującą metodę: jeżeli chcemy wykazać, że dla liczby naturalnej \(n\) liczba \(\sqrt{n}\) jest wymierna, wystarczy znaleźć taką liczbę pierwszą \(p\), że \(n\) jest podzielne przez \(p\) i jest podzielna przez \(p^2\). W ten sposób można na przykład stwierdzić, że liczba \(\sqrt{18}\) nie jest wymierna, bo 18 jest podzielne przez 2, ale nie jest podzielna przez 4.
Od kiedy używa się liczb wymiernych?
Liczby wymierne były już w użyciu w starożytnym Egipcie w XVII p.n.e.
Kalkulator

Skracanie ułamków zwykłych
W tym miejscu możesz zobaczyć, w jaki sposób skracamy ułamki zwykłe. Nasz robot rozwiązuje dowolne zadanie z tego zakresu.
Wpisz dane:Licznik:
Mianownik:
Objaśnienia:
- Jeżeli wynik wskaże wartość „infinity”, to oznacza, że jest poza zakresem dostępnym dla niniejszego kalkulatora.
- Zapis wyniku 1.2e+12 oznacza liczbę 1.2 pomnożoną przez 1012.
- Gdy jedna z liczb będąca wynikiem działań jest większa od jej reprezentacji 64-bitowej, kalkulator stosuje przybliżenia wyniku.
- Jeżeli podasz liczbę rzeczywistą, do obliczeń zostanie wzięta jedynie jej część całkowita.
Zadania z rozwiązaniami

Zadanie nr 1.
Sprawdzić, czy liczba \(5,35(43)\) jest wymierna czy niewymierna.

Zadanie nr 2 — maturalne.
Równość \(\frac{1}{4}+\frac{1}{5}+\frac{1}{a}=1\) jest prawdziwa dla
A. \(a=\frac{11}{20}\)
B. \(a=\frac{8}{9}\)
C. \(a=\frac{9}{8}\)
D. \(a=\frac{20}{11}\)

Zadanie nr 3.
Wykaż, że podane liczby są liczbami wymiernymi:
A. 1
B. 0,(32)
C. -1000
D. 1,012

Zadanie nr 4.
Wykaż cztery liczby wymierne między \(0,2\) a \(\frac{3}{11}\).

Zadanie nr 5 — maturalne.
Różnica \(0,(3)-\frac{23}{33}\) jest równa
A. \(-0,(39)\)
B. \(-\frac{39}{100}\)
C. \(-0,36\)
D. \(-\frac{4}{11}\)
Wybrane karty pracy
Powiązane materiały
 Liczby wymierne
Liczby wymierne Liczby — quiz
Liczby — quiz© medianauka.pl, 2008-10-17, A-86
Data aktualizacji artykułu: 2023-02-18

 Liczby naturalne
Liczby naturalne Liczby całkowite
Liczby całkowite Liczby niewymierne
Liczby niewymierne Liczby rzeczywiste
Liczby rzeczywiste Kres górny i kres dolny zbioru
Kres górny i kres dolny zbioru Przedziały liczbowe
Przedziały liczbowe Zbiór liczb rzeczywistych i jego podzbiory
Zbiór liczb rzeczywistych i jego podzbiory Ułamek liczby — quiz
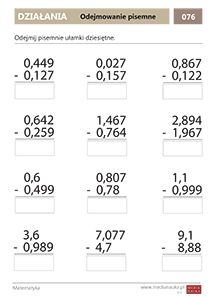
Ułamek liczby — quiz Odejmowanie ułamków dziesiętnych
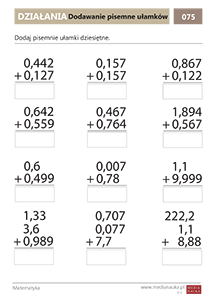
Odejmowanie ułamków dziesiętnych Dodawanie ułamków dziesiętnych
Dodawanie ułamków dziesiętnych Porównywanie ułamków dziesiętnych
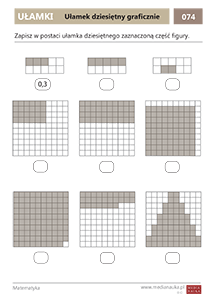
Porównywanie ułamków dziesiętnych Zamiana na ułamki dziesiętne
Zamiana na ułamki dziesiętne