Liczby rzeczywiste

Co to jest liczba rzeczywista?

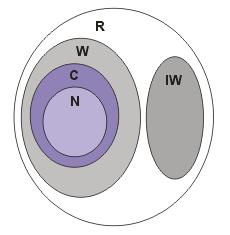
Zbiór liczb rzeczywistych jest to suma zbioru liczb wymiernych i zbioru liczb niewymiernych. Zbiór liczb rzeczywistych oznaczamy symbolem \(\mathbb{R}\)

Zatem \(\mathbb{Q}\cup \mathbb{IQ}=\mathbb{R}\)

Przykłady liczb rzeczywistych

Przykładem liczby rzeczywistej jest dowolna liczba wymierna lub niewymierna. Są to więc na przykład liczby: 0, 1, 12347593, -4564, \(frac{1}{2}\), 0,445, 3,(3), \(\pi\), \(\sqrt{2}\), \(\sqrt{5}\), \(1-2\sqrt{2}\), e (podstawa logarytmu naturalnego) i nieskończenie wiele innych liczb.

Co więcej, liczb rzeczywistych między dwiema liczbami naturalnymi, na przykład 0 i 1, również jest nieskończenie wiele. Liczby rzeczywiste spełniają aksjomat ciągłości. Mówiąc bardzo obrazowo oznacza to, że nie ma luk między liczbami na osi liczbowej.

Własności liczb rzeczywistych

Zbiór liczb rzeczywistych jest zupełny.

Moc zbioru \(\mathbb{R}\) jest większa niż moc zbioru liczb naturalnych\(\mathbb{N}\).

Zbiór liczb rzeczywistych jest nieprzeliczalny. Oznacza to, że nie istnieje taki ciąg, który zawierałby wszystkie liczby rzeczywiste.

Liczby rzeczywiste można utożsamić z punktami na prostej (osi liczbowej).

Działania na liczbach rzeczywistych

W zbiorze liczb rzeczywistych wykonywalne są następujące działania:

dodawanie;
odejmowanie;
mnożenie;
dzielenie.

Relacje

W zbiorze \(\mathbb{R}\) określone są relacje nierówności mocne (ostre):

„>” (większe);
„<” (mniejsze);

oraz nierówności słabe (nieostre):

„≥” (większe lub równe);
„≤” (mniejsze lub równe);

oraz znak relacja równości „=”.

Ciekawostki

Istnieje więcej niż jedna konstrukcja (definicji) zbioru liczb rzeczywistych. Jedna z najbardziej popularnych definicji (Cantora) opiera się klasach ciągów liczb, które spełniają warunek Cauchy'ego. W konstrukcji \(\mathbb{R}\) rozpatruje się zbieżności tych ciągów.

Pytania

Czy 0 jest liczbą rzeczywistą?

Tak, zero jest liczbą rzeczywistą. Należy przy tym także do zbioru liczb wymiernych, całkowitych i naturalnych (w zależności o przyjętej umowy).

Czy w zbiorze liczb rzeczywistych istnieje taka liczba, która nie jest ani liczbą wymierną, ani liczbą niewymierną?

Nie. Ponieważ zbiór R jest sumą zbioru liczb wymiernych i niewymiernych, nie ma w nim innych liczb.

Czy istnieją liczby. które nie są liczbami rzeczywistymi?

Tak, to na przykład liczby zespolone.

Kiedy odkryto liczby rzeczywiste?

Już w starożytnej Grecji zdawano sobie sprawę z istnienia liczb niewymiernych. Długość przekątnej kwadratu o boku 1 była tego przykładem

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.