Liczby niewymierne

Co to jest liczba niewymierna?

Liczba niewymierna jest to liczba rzeczywista, której nie można wyrazić w postaci \(\frac{a}{b},b\neq 0\), gdzie a jest liczbą całkowitą i b jest liczbą całkowitą różną od zera.

Zbiór liczb niewymiernych oznaczamy symbolem \(\mathbb{IQ}\). Dawniej zbiór liczb niewymiernych oznaczano symbolem \(\mathbb{IW}\).

Przykłady

Oto przykłady liczb niewymiernych:

Oto przykłady liczb niewymiernych: \(\sqrt{2}, \sqrt{3}, e, \pi, \sqrt{11}+11\).

Własności liczb niewymiernych

Rozwinięcie dziesiętne liczby niewymiernej jest nieskończone i nieokresowe.

Działania na liczbach niewymiernych

W zbiorze liczb niewymiernych wykonywalne są następujące działania:

dodawanie;
odejmowanie;
mnożenie;
dzielenie.

Ponadto prawdziwe są twierdzenia:

Suma liczby niewymiernej i wymiernej jest niewymierna.
Iloczyn dwóch liczb niewymiernych może być liczbą wymierną albo niewymierną.

Przykłady

\(2+2\sqrt{2}\) jest liczbą niewymierną.
\(\sqrt{11}-11\) jest liczbą niewymierną.
\(\sqrt{4}=2\) jest liczbą wymierną.
\(\sqrt{2}\cdot \sqrt{2}=\sqrt{4}=2 \) jest liczbą wymierną.
\(\sqrt{2}\cdot \sqrt{3}=\sqrt{6} \) jest liczbą niewymierną.

Zbiór liczb niewymiernych

Liczby wymierne nie są wystarczające chociażby do mierzenia długości odcinków. Zbiór wszystkich takich liczb, nazywamy zbiorem liczb niewymiernych. Liczba niewymierna może być dodatnia, a także ujemna. Liczb niewymiernych jest nieskończenie wiele.

Możemy powiedzieć, że liczby niewymierne to liczby rzeczywiste niebędące liczbami wymiernymi. Są to więc takie liczby rzeczywiste, których nie można zapisać w postaci ilorazu dwóch liczb: liczby całkowitej przez liczbę całkowitą różną od zera.

Zbiór liczb niewymiernych i zbiór liczb wymiernych tworzą razem zbiór liczb rzeczywistych.

Dowód

Wykażemy, że długość przekątnej kwadratu o boku długości 1 jest liczbą niewymierną.

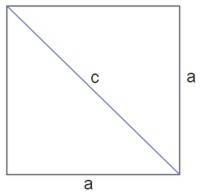
Dane jest \(a=1\). Na podstawie twierdzenia Pitagorasa możemy zapisać:

\(1^2+ 1^2= c^2\)

\(c^2= 2\).

Załóżmy, że \(c\) jest liczbą wymierną, czyli, że da się wyrazić za pomocą ułamka \(\frac{m}{n}, n\neq 0\). Wtedy:

\((\frac{m}{n})^2=2\)

\(\frac{m^2}{n^2}=2/\cdot n^2 (n\neq 0)\)

\(m^2=2n^2\)

\(m\cdot m = 2\cdot n\cdot n\)

Można próbować rozłożyć liczby po obu stronach równania na czynniki i zauważyć, że po lewej stronie równania czynnik 2 nie występuje lub występuje parzystą liczbę razy. Po prawej stronie równania czynnik 2 występuje zawsze w nieparzystej liczbie. Powyższa równość zatem nie może być spełniona. Założenie, że c jest liczbą wymierną jest więc błędne.

Pytania

Jak sprawdzić, czy liczba jest niewymierna?

Najczęściej stosuje się dowód nie wprost, czyli założenie, że dana liczba jest wymierna, czyli że da się wyrazić w postaci ilorazu dwóch liczb całkowitych \(\frac{p}{q}\), przy czym \(q\) jest różne od zera i poprzez dochodzenie do sprzeczności można wykazać, że dana liczba nie jest wymierna.

Dla pierwiastków można zastosować następującą metodę: jeżeli chcemy wykazać, że dla liczby naturalnej \(n\) liczba \(\sqrt{n}\) jest wymierna, wystarczy znaleźć taką liczbę pierwszą \(p\), że \(n\) jest podzielne przez \(p\) i nie jest podzielna przez \(p^2\). W ten sposób można na przykład stwierdzić, że liczba \(sqrt{18}\) nie jest wymierna, bo 18 jest podzielne przez 2, ale nie jest podzielna przez 4.

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.