Działania matematyczne

W tym rozdziale omawiamy działania arytmetyczne, a więc działania na liczbach rzeczywistych, przyporządkowujące dwóm określonym liczbom trzecią liczbę. Są to dodawanie, odejmowanie, mnożenie i dzielenie. W tym miejscu omawiamy także inne rodzaje działań w matematyce, w tym potęgowanie, pierwiastkowanie. Definiujemy logarytm naturalny i dziesiętny. Omawiamy też, w jaki sposób obliczyć procent danej liczby, czym są procenty i promile. Wprowadzamy także pewne pojęcia algebry, w tym macierze i wyznaczniki. Objaśniamy zasady wykonywania kolejności wykonywania działań.

Spis treści

Dodawanie i odejmowanie

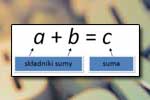DodawanieDodawanie
OdejmowanieOdejmowanie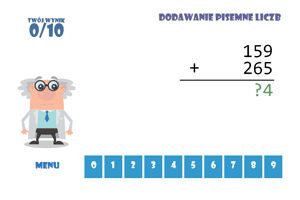
Dodawanie pisemne liczbDodawanie pisemne
Odejmowanie pisemne liczbOdejmowanie pisemne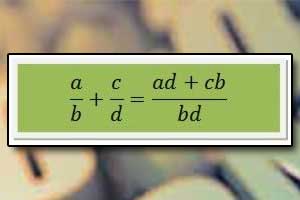
Dodawanie ułamkówDodawanie ułamków
Odejmowanie ułamkówOdejmowanie ułamków
Symbol SIGMASymbol SIGMA
testTest z dodawania
testTest z odejmowania
testZadania — dodawanie
testZadania — odejmowanie

Mnożenie i dzielenie

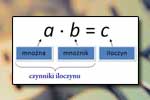IloczynIloczyn
Dzielenie liczbDzielenie liczb
Tabliczka mnożeniaTabliczka mnożenia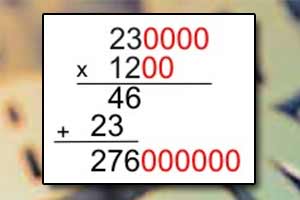
Mnożenie pisemneMnożenie pisemne liczb
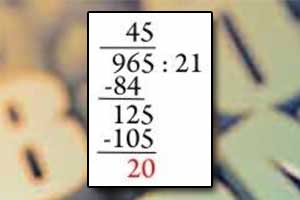Dzielenie pisemneDzielenie pisemne
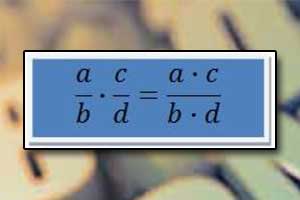Mnożenie ułamkówMnożenie ułamków
Dzielenie ułamków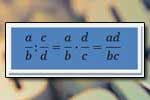Dzielenie ułamków
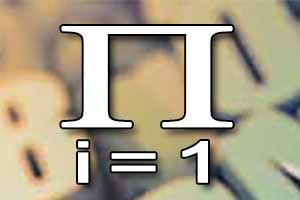Symbol piSymbol pi
testTest z mnożenia
testTest z dzielenia
testZadania — mnożenie
testZadania — dzielenie

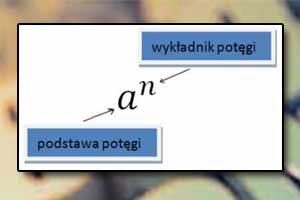Potęgowanie

PotęgowaniePotęgowanie
Działania na potęgachDziałania na potęgach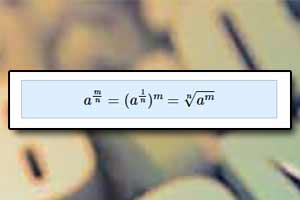
Potęga o wykładniku wymiernymPotęga o wykładniku wymiernym
Potęga o wykładniku niewymiernymPotęga o wykładniku niewymiernym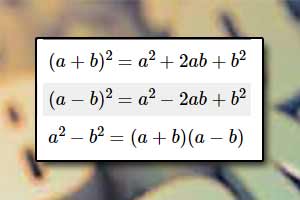
Wzory skróconego mnożeniaWzory skróconego mnożenia
Wzór dwumianowy NewtonaWzór dwumianowy Newtona
testTest z podstaw potęgowania
testTest — Potęga o wykładniku wymiernym i niewymiernym
testTest ze wzorów skróconego mnożenia
testZadania — potęgowanie

Pierwiastkowanie

Pierwiastek arytmetycznyPierwiastek arytmetyczny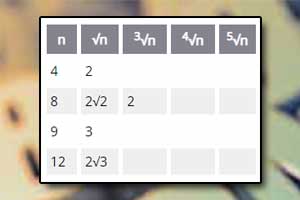
Wyłączanie czynnika przed pierwiastekWyłączanie czynnika przed pierwiastek
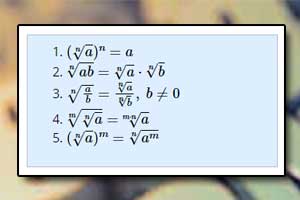Działania na pierwiastkachDziałania na pierwiastkach
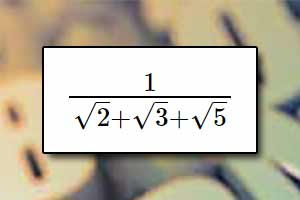Usuwanie niewymierności z mianownikaUsuwanie niewymierności z mianownika
testTest z pierwiastków
testZadania — pierwiastki

Logarytmowanie

LogarytmLogarytm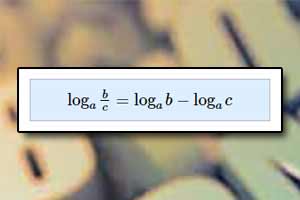
Własności logarytmówWłasności logarytmów
testTest z logarytmów
testZadania z logarytmów

Procenty

ProcentProcent
PromilPromil
testTest z procentów
testZadania z procentów

Macierze i wyznaczniki

MacierzMacierz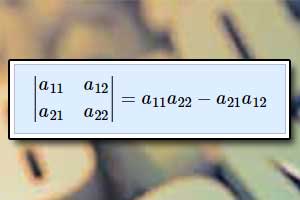
Wyznacznik macierzyWyznacznik macierzy

Inne materiały

Wartość bezwzględnaWartość bezwzględna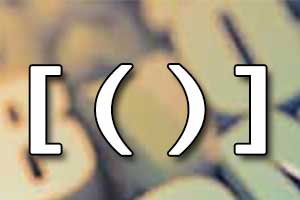
Kolejność wykonywania działańKolejność wykonywania działań
Silnia n!Silnia n!
Symbol NewtonaSymbol Newtona
testTest — silnia i symbol Newtona
testZadania — inne działania

SPIS TREŚCI





© medianauka.pl, 2018-02-19, A-3538
Data aktualizacji artykułu: 2023-01-30



Udostępnij
©® Media Nauka 2008-2023 r.