Potęgowanie
Co to jest potęga danej liczby? W artykule zamieszczamy definicję potęgi i przykłady potęgowania. Własności potęgowania omawiamy w kolejnym artykule.
Definicja
Potęgę o podstawie \(a\) i wykładniku naturalnym \(n\) oznaczamy przez \(a^n\) i określamy w następujący sposób:
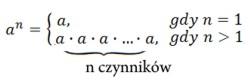
Przykłady
\(5^1=5\)
\(5^2=5\cdot 5=25\)
\( 5^3=5\cdot 5\cdot 5=125\)
\( 5^4=5\cdot 5\cdot 5\cdot 5=625\)
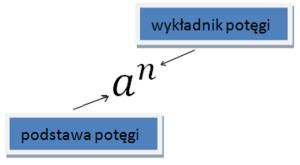
Podstawa i wykładnik potęgi
Podstawa potęgi jest to liczba, którą podnosimy do potęgi. Wykładnik potęgi jest to liczba, do której potęgi podnosimy podstawę.
Zapamiętaj, że:
Potęga o wykładniku ujemnym
Możemy rozszerzyć powyższą definicję dla wykładnika całkowitego w następujący sposób:
Dla \(a\neq 0, m \in \mathbb{C}\):
\(a^0=1\)
\( a^{-m}=\frac{1}{a^m}\)
Przykłady
- \(2^0=1\)
- \((-1)^0=1\)
- \(133,5^0=1\)
- \((\frac{3}{4})^0=1\)
- \(2^{-1}=\frac{1}{2}\)
- \((-3)^{-1}=-\frac{1}{3}\)
- \((\frac{7}{8})^{-1}=\frac{8}{7}\)
- \(2^{-3}=\frac{1}{2^3}=\frac{1}{8}\)
Zero do potęgi zerowej
Kwadrat i sześcian liczby
Działania na potęgach, takie jak mnożenie potęg, dzielenie potęg, potęgowanie ułamków, a także inne przydatne wzory na potęgowanie omawiamy w kolejnym artykule.
Odwrotność potęgowania
Działanie odwrotne do potęgowania to pierwiastkowanie.
Potęgowanie liczb ujemnych
Każda liczba ujemna podniesiona do potęgi o wykładniku parzystym jest liczbą dodatnią.
Przykłady
- \((-1)^2=1\)
- \((-1)^{2000}=1\)
- \((-2)^{2}=4\)
- \((-\frac{1}{2})^{4}=\frac{1}{16}\)
Każda liczba ujemna podniesiona do potęgi o wykładniku nieparzystym jest liczbą ujemną.
Przykłady
- \((-1)^3=-1\)
- \((-1)^{2001}=-1\)
- \((-2)^{3}=-4\)
- \((-\frac{1}{2})^{3}=-\frac{1}{8}\)
Kalkulator

Potęgowanie — kalkulator
W tym miejscu możesz wykonać potęgowanie na liczbach.
Wpisz podstawę i wykładnik potęgi:n ^k
Pytania
Jak potęgujemy ułamki?
Potęgowanie ułamków omawiamy w artykule o działaniach na potęgach.
Jak potęgujemy pierwiastki?
Potęgowanie pierwiastków omawiamy w artykule o działaniach na pierwiastkach.
Jak potęgujemy potęgi?
Potęgowanie potęgi omawiamy w artykule o działaniach na potęgach.
Jak potęgujemy logarytmy?
Potęgowanie logarytmów omawiamy w artykule o logarytmach.
Jak przebiega potęgowanie nawiasów?
Aby podnieść do kwadratu lub sześcianu wyrażenie w nawiasie, korzystamy ze wzorów skróconego mnożenia. Dla wyższych potęg warto poznać wzór dwumianowy Newtona.
Jak zrealizować potęgowanie w Excelu?
Aby obliczyć potęgę, korzystamy z operatora „^”. Jeżeli w dowolnej komórce wpiszemy "=2^10", to otrzymamy dziesiątą potęgę liczby 2.
Można także skorzystać z funkcji POTĘGA. Jeżeli w komórce A1 wpiszemy liczbę 2, w komórce A2 liczbę 3, a w komórce A3 formułę "=POTĘGA(A1;A2)", to otrzymamy wynik potęgowania \(2^3=8\).

Tabela potęgowania
| n | \(2^n\) | \(3^n\) | \(4^n\) | \(5^n\) |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 4 | 9 | 16 | 25 |
| 3 | 8 | 27 | 64 | 125 |
| 4 | 16 | 81 | 256 | 625 |
| 5 | 32 | 243 | 1024 | 3125 |
| 6 | 64 | 729 | 4096 | 15625 |
| 7 | 128 | 2187 | 16384 | 78125 |
| 8 | 256 | 6561 | 65536 | 390625 |
| 9 | 512 | 19683 | 262144 | 1953125 |
| 10 | 1024 | 59049 | 1048576 | 9765625 |
| 11 | 2048 | 177147 | 4194304 | 48828125 |
| 12 | 4096 | 531441 | 16777216 | 244140625 |
| 13 | 8192 | 1594323 | 67108864 | 1220703125 |
| 14 | 16384 | 4782969 | 268435456 | 6103515625 |
| 15 | 32768 | 14348907 | 1073741824 | 30517578125 |
| 16 | 65536 | 43046721 | 4294967296 | 152587890625 |
| 17 | 131072 | 129140163 | 17179869184 | 762939453125 |
| 18 | 262144 | 387420489 | 68719476736 | 3814697265625 |
| 19 | 524288 | 1162261467 | 274877906944 | 19073486328125 |
| 20 | 1048576 | 3486784401 | 1099511627776 | 95367431640625 |
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Liczba \(\Bigl(\frac{1}{(\sqrt[3]{729}+\sqrt[4]{256}+2)^0}\Bigr)^{-2}\) jest równa:
A. \(\frac{1}{125}\)
B. \(\frac{1}{15}\)
C. \(1\)
D. \(15\).
Wybrane karty pracy
Powiązane materiały
 Potęgowanie
Potęgowanie© medianauka.pl, 2009-01-16, A-143
Data aktualizacji artykułu: 2023-03-11


 Potęgi
Potęgi Działania na potęgach
Działania na potęgach Pierwiastek arytmetyczny
Pierwiastek arytmetyczny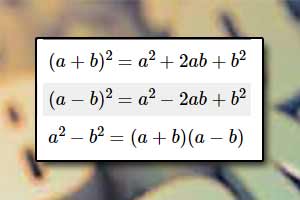 Wzory skróconego mnożenia
Wzory skróconego mnożenia Wzór dwumianowy Newtona
Wzór dwumianowy Newtona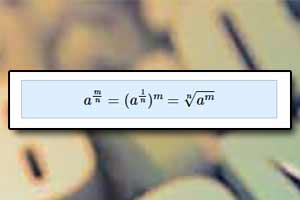 Potęga o wykładniku wymiernym
Potęga o wykładniku wymiernym Potęga o wykładniku niewymiernym
Potęga o wykładniku niewymiernym Potęgowanie — quiz
Potęgowanie — quiz Trzecia potęga — quiz
Trzecia potęga — quiz Druga potęga — quiz
Druga potęga — quiz