Pierwiastek arytmetyczny

Pierwiastek stopnia \(n\) z liczby \(a \geq 0\) oznaczamy symbolem \(\sqrt[n]{a}\) i definiujemy w następujący sposób:

\(\sqrt[n]{a}\Leftrightarrow b^n=a, b\geq 0\)

Przykłady

\(\sqrt[3]{27}=3\), bo \(3^3=27\).
\(\sqrt[8]{256}=2\), bo \(2^8=256\).

Widzimy zatem, że pierwiastkowanie jest działaniem odwrotnym do potęgowania.

Pierwiastek kwadratowy

Pierwiastek drugiego stopnia nazywamy też pierwiastkiem kwadratowym i zamiast pisać \(\sqrt[2]{a}\) piszemy \(\sqrt{a}\).

Pierwiastek sześcienny

Pierwiastek trzeciego stopnia nazywamy też pierwiastkiem sześciennym.

Pierwiastek 3 stopnia zapisujemy następująco: \(\sqrt[3]{a}\).

Zgodnie z definicją pierwiastek arytmetyczny istnieje jedynie dla liczb nieujemnych i jest również liczbą nieujemną.

W dalszej części artykułu poznamy działania na pierwiastkach i ich zastosowanie.

Pytania

Ile wynosi pierwiastek z 0?

Pierwiastek dowolnego stopnia z zera jest równy zeru.

Jak obliczyć pierwiastek w programie Excel?

W Excelu korzystamy z funkcji PIERWIASTEK. W dowolnej komórce napisz formułę „=PIERWIASTEK(12)”, a otrzymasz wynik pierwiastka z liczby 12.

Możesz także skorzystać z operatora potęgi „^”. Powyższy efekt uzyskasz wpisując formułę „=12^(1/2)”.

Czy istnieje pierwiastek z liczby ujemnej?

Nie istnieje pierwiastek z liczby ujemnej w zbiorze liczb rzeczywistych. Pierwiastki takie oblicza się jednak w zbiorze liczb zespolonych.

Jak obliczyć pierwiastek 3 stopnia na kalkulatorze?

Wystarczy podnieść liczbę do potęgi 1/3.

Jak obliczyć pierwiastek z pierwiastka?

Korzystamy z działań na pierwiastkach: \(\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}\).

Tablica pierwiastków

Tablica
Poniżej przedstawiamy wartości lub przybliżenia pierwiastków kwadratowych lub sześciennych wybranych (3 stopnia) liczb naturalnych.

Pierwiastek z 5, pierwiastek z 3 i pierwiastek z 2 został wyróżniony w tabeli czerwoną czcionką.

n	Pierwiastek kwadratowy	Pierwiastek sześcienny
1	1	1
2	1,41421356237310	1,25992104989487
3	1,73205080756888	1,44224957030741
4	2	1,58740105196820
5	2,23606797749979	1,70997594667670
6	2,44948974278318	1,81712059283214
7	2,64575131106459	1,91293118277239
8	2,82842712474619	2
9	3,00000000000000	2,08008382305190
10	3,16227766016838	2,15443469003188
11	3,31662479035540	2,22398009056932
12	3,46410161513775	2,28942848510666
13	3,60555127546399	2,35133468772076
14	3,74165738677394	2,41014226417523
15	3,87298334620742	2,46621207433047
16	4	2,51984209978975
17	4,12310562561766	2,57128159065824
18	4,24264068711928	2,62074139420890
19	4,35889894354067	2,66840164872194
20	4,47213595499958	2,71441761659491

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.

ĆWICZENIA

Pierwiastek arytmetyczny

Powiązane quizy

Pierwiastek

Szkoła podstawowa
Klasa 7
Liczba pytań: 15

Inne zagadnienia z tej lekcji

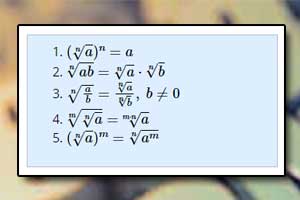Działania na pierwiastkach

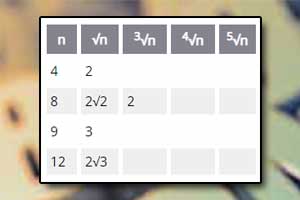Wyłączanie czynnika przed pierwiastek

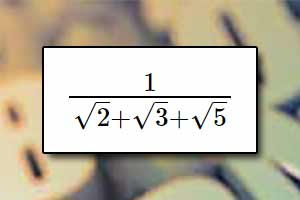Usuwanie niewymierności z mianownika

Pierwiastkowanie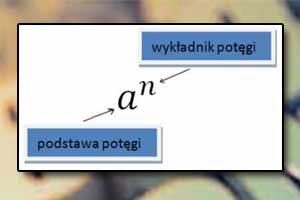

Potęgowanie