Wyłączanie czynnika przed pierwiastek

Tablica - wyłączanie czynnika przed pierwiastek

Poniższa tabela zawiera te liczby, dla których z pierwiastków stopnia od 2 do 5 tych liczb można wyłączyć czynnik przed pierwiastek.

n	√n	³√n	⁴√n	⁵√n
4	2
8	2√2	2
9	3
12	2√3
16	4	2³√2	2
18	3√2
20	2√5
24	2√6	2³√3
25	5
27	3√3	3
28	2√7
32	4√2	2³√4	2⁴√2	2
36	6
40	2√10	2³√5
44	2√11
45	3√5
48	4√3	2³√6	2⁴√3
49	7
50	5√2
52	2√13
54	3√6	3³√2
56	2√14	2³√7
60	2√15
63	3√7
64	8	4	2⁴√4	2⁵√2
68	2√17
72	6√2	2³√9
75	5√3
76	2√19
80	4√5	2³√10	2⁴√5
81	9	3³√3	3
84	2√21
88	2√22	2³√11
90	3√10
92	2√23
96	4√6	2³√12	2⁴√6	2⁵√3
98	7√2
99	3√11
100	10
104	2√26	2³√13
108	6√3	3³√4
112	4√7	2³√14	2⁴√7
116	2√29
117	3√13
120	2√30	2³√15
121	11
124	2√31
125	5√5	5
126	3√14
128	8√2	4³√2	2⁴√8	2⁵√4
132	2√33
135	3√15	3³√5
136	2√34	2³√17
140	2√35
144	12	2³√18	2⁴√9
147	7√3
148	2√37
150	5√6
152	2√38	2³√19
153	3√17
156	2√39
160	4√10	2³√20	2⁴√10	2⁵√5
162	9√2	3³√6	3⁴√2
164	2√41
168	2√42	2³√21
169	13
171	3√19
172	2√43
175	5√7
176	4√11	2³√22	2⁴√11
180	6√5
184	2√46	2³√23
188	2√47
189	3√21	3³√7
192	8√3	4³√3	2⁴√12	2⁵√6
196	14
198	3√22
200	10√2	2³√25

Bardzo duże znaczenie praktyczne ma tak zwane wyłączanie czynnika przed pierwiastek. Z własności działań na pierwiastkach mamy:

$\sqrt[n]{a^n\cdot b}=\sqrt[n]{a^n}\cdot \sqrt[n]{b}=a\sqrt[n]{b},\ a\geq0,\ b\geq 0$

Aby wyłączyć czynnik przed pierwiastek należy więc liczbę pod pierwiastkiem sprowadzić do postaci: a ⁿ∙b

Przyjrzyjmy się zatem przykładom.

Przykłady

$\sqrt[3]{54}=\sqrt[3]{27\cdot 2}=\sqrt[3]{3^3\cdot 2}=\sqrt[3]{3^3}\cdot \sqrt[3]{2}=3\sqrt[3]{2}\\ \sqrt{24}=\sqrt{4\cdot 6}=\sqrt{4}\cdot \sqrt{6}=2\sqrt{6}$

Powyższe przykłady dotyczą małych liczb. Co zrobić, gdy mamy do czynienia z dużymi liczbami pod pierwiastkiem? Korzystamy wówczas z rozkładu liczby na czynniki pierwsze. Następnie zakreślamy po tyle samo liczb pierwszych (najlepiej w różny sposób kolejne grupy) ile wynosi stopień pierwiastka i mnożymy przez siebie po jednej z każdej grupy otrzymując w ten sposób liczbę a ze wzoru a ⁿ∙b. Liczbę b stanowi iloczyn niezakreślonych liczb pierwszych.

Opisany wyżej sposób ilustruje poniższy przykład.

Przykład

Obliczamy $\sqrt[3]{1296}$ .

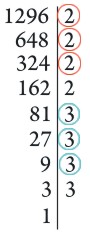Rozkładamy więc liczbę 1296 na czynniki pierwsze i ponieważ obliczamy pierwiastek trzeciego stopnia zaznaczamy grupy takich samych liczb po 3 tak, jak to ilustruje rysunek.
Zgodnie z powyższą procedurą mamy a = 2 ∙ 3 = 6 (z zakreślonych liczb) oraz b = 2 ∙ 3 = 6 (z pozostałych niezakreślonych liczb). Zatem 1296 = 6 ³ ∙ 6. Z tego $\sqrt[3]{1296}=\sqrt[3]{6^3\cdot 6}=6\sqrt[3]{6}$ .

Powyższa procedura jest prosta, ale ma jedną wadę - trzeba ją pamiętać.
Można więc po prostu skorzystać z prostego rachunku, aby uzyskać ten sam wynik.

Z rozkładu na czynniki pierwsze oraz z działań na potęgach wiemy:
1296=2∙2∙2∙2∙3∙3∙3∙3=2³∙2∙3³∙3=6³∙6

Warto poćwiczyć wyłączanie czynnika przed pierwiastek, ponieważ spotkasz się z tym praktycznie na każdym kroku podczas rozwiązywania zadań. Proponuję aby wyjąć czynnik przed pierwiastek stopnia drugiego, trzeciego, czwartego i piątego dowolnej liczby z zakresu od 10 do 10000 i sprawdzić wynik w tablicach zamieszczonych w niniejszym artykule.

Kalkulator
W tym miejscu możesz sprawdzić, czy można wyłączyć całkowity czynnik przed pierwiastek dla danej liczby naturalnej.

Wpisz liczbę:

Pytania

Jakie pierwiastki pojawiają się w zadaniach najczęściej?

Odpowiedź podzielimy na trzy części.

Pierwsza z nich to pierwiastki, z których można wyłączyć całkowity czynnik przed pierwiastek:

pierwiastek z 8, wynik 2√2;
pierwiastek z 12, wynik 2√3;
pierwiastek z 18, wynik 3√2;
pierwiastek z 20, wynik 2√5;
pierwiastek z 24, wynik 2√6;
pierwiastek z 32, wynik 4√2;
pierwiastek z 40, wynik 2√10;
pierwiastek z 48, wynik 4√3;
pierwiastek z 50, wynik 5√2;
pierwiastek z 72, wynik 6√2;
pierwiastek z 80, wynik 4√5;
pierwiastek z 108, wynik 6√3;
pierwiastek z 128, wynik 8√2;
pierwiastek z 180, wynik 6√5;
pierwiastek z 216, wynik 6√6;

Druga z nich to pierwiastki, które dają wynik całkowity:

√0=0;
√1=1;
√4=2;
√36=6;
√144=12;
√289=17;
√225=15;

Trzecia z nich to pierwiastki, dla których podajemy przybliżone wyniki w tablicy, którą znajdziesz tutaj.

Zadania z rozwiązaniami

Zadania związane z tematem:
Wyłączanie czynnika przed pierwiastek

Zadanie - wyłączanie czynnika przed pierwiastek
Uprościć ułamek
a) $\frac{\sqrt[4]{6480}}{6}$
b) $\frac{\sqrt{12}+\sqrt{32}-\sqrt{20}-\sqrt{24}}{2}$

Pokaż rozwiązanie zadania

Zadanie - wyłączanie czynnika przed pierwiastek
Obliczyć bez użycia kalkulatora:
a) $\sqrt{1764}$
b) $\sqrt[3]{2376}$

Pokaż rozwiązanie zadania

Zadanie maturalne nr 2, matura 2017
Liczba $\sqrt[3]{54}-\sqrt[3]{2}$ jest równa :

A. $\sqrt[3]{52}$
B. 3
C. $\sqrt[3]{2}$
D. 2

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Pierwiastek arytmetyczny
Definicja pierwiastka arytmetycznego, quiz - pierwiastkowanie, przykłady obliczania pierwiastka z danej liczby.

Działania na pierwiastkach
Wzory na działania na pierwiastkach, przykłady stosowania, zadania z rozwiązaniami, dodawanie, odejmowanie pierwiastków

Usuwanie niewymierności z mianownika
Usuwanie niewymierności z mianownika wyrażenia polega na takim przekształceniu wyrażenia, aby w mianowniku otrzymać liczbę wymierną.

Test wiedzy

Wyłączanie czynnika przed pierwiastek

Tablica - wyłączanie czynnika przed pierwiastek

Pytania

Zadania z rozwiązaniami

Inne zagadnienia z tej lekcji

Bibliografia