Tablice matematyczne
W tym miejscu zgromadziliśmy odnośniki to tablic matematycznych zawartych w treści poszczególnych artykułów i lekcji. Są to zestawienia przydatnych danych oraz oznaczeń stosowanych w matematyce.
Spis treści
Poniżej prezentujemy wykaz wszystkich opublikowanych tablic tematycznych z podziałem na poszczególne działy:
Wybrane materiały podręczne - na skróty
Interaktywna karta wzorów i interaktywne tablice matematyczne
Tutaj znajduje się indeks pojęć, dla których można znaleźć w serwisie wzory oraz tablice.
 Symbole i oznaczenia w matematyce
Symbole i oznaczenia w matematyce
Wykaz oznaczeń i symboli stosowanych w matematyce wraz z linkami do artykułów.
 Tablice matematyczne CKE
Tablice matematyczne CKEOdnośnik do strony Centralnej Komisji Egzaminacyjnej (CKE) z kartą wzorów i tablic - Wybrane wzory matematyczne. Dokument jest w formacie PDF.
Liczby i działania
Wartość bezwzględna liczby
| Definicja | Własności | Więcej |
|---|---|---|
|
Przejdź do artykułu Wartość bezwzględna. |
Silnia
| Definicja | Własności | Więcej |
|---|---|---|
Silnia, oznaczana symbolem wykrzyknika. 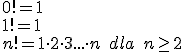 | (n+1)!=n!(n+1) | Przejdź do artykułu silnia. |
Tablica silni
Poniżej wyniki silni dla pierwszych 50 liczb naturalnych.
| 0! | = 1 |
| 1! | = 1 |
| 2! | = 2 |
| 3! | = 6 |
| 4! | = 24 |
| 5! | = 120 |
| 6! | = 720 |
| 7! | = 5040 |
| 8! | = 40320 |
| 9! | = 362880 |
| 10! | = 3628800 |
| 11! | = 39916800 |
| 12! | = 479001600 |
| 13! | = 6227020800 |
| 14! | = 87178291200 |
| 15! | = 1307674368000 |
| 16! | = 20922789888000 |
| 17! | = 355687428096000 |
| 18! | = 6402373705728000 |
| 19! | = 121645100408832000 |
| 20! | = 2432902008176640000 |
| 21! | = 51090942171709440000 |
| 22! | = 1124000727777607680000 |
| 23! | = 25852016738884976640000 |
| 24! | = 620448401733239439360000 |
| 25! | = 15511210043330985984000000 |
| 26! | = 403291461126605635584000000 |
| 27! | = 10888869450418352160768000000 |
| 28! | = 304888344611713860501504000000 |
| 29! | = 8841761993739701954543616000000 |
| 30! | = 265252859812191058636308480000000 |
| 31! | = 8222838654177922817725562880000000 |
| 32! | = 263130836933693530167218012160000000 |
| 33! | = 8683317618811886495518194401280000000 |
| 34! | = 295232799039604140847618609643520000000 |
| 35! | = 10333147966386144929666651337523200000000 |
| 36! | = 371993326789901217467999448150835200000000 |
| 37! | = 13763753091226345046315979581580902400000000 |
| 38! | = 523022617466601111760007224100074291200000000 |
| 39! | = 20397882081197443358640281739902897356800000000 |
| 40! | = 815915283247897734345611269596115894272000000000 |
| 41! | = 33452526613163807108170062053440751665152000000000 |
| 42! | = 1405006117752879898543142606244511569936384000000000 |
| 43! | = 60415263063373835637355132068513997507264512000000000 |
| 44! | = 2658271574788448768043625811014615890319638528000000000 |
| 45! | = 119622220865480194561963161495657715064383733760000000000 |
| 46! | = 5502622159812088949850305428800254892961651752960000000000 |
| 47! | = 258623241511168180642964355153611979969197632389120000000000 |
| 48! | = 12413915592536072670862289047373375038521486354677760000000000 |
| 49! | = 608281864034267560872252163321295376887552831379210240000000000 |
| 50! | = 30414093201713378043612608166064768844377641568960512000000000000 |
Symbol Newtona, współczynnik dwumianowy
| Definicja | Własności | Więcej |
|---|---|---|
Niech
lub
|
|
Przejdź do artykułu symbol Newtona. |
Wzór dwumianowy Newtona
| Definicja | Własności | Więcej |
|---|---|---|
|
Brak | Przejdź do artykułu Wzór dwumianowy Newtona. |
Wzory skróconego mnożenia
| Definicja | Własności | Więcej |
|---|---|---|
Wzór na kwadrat sumy
Wzór na sześcian sumy
|
Brak | Przejdź do artykułu Wzory skróconego mnożenia. |
Potęgowanie
| Definicja | Własności | Więcej |
|---|---|---|
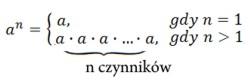 Potęga o wykładniku wymiernym: Dla a - liczby nieujemnej, m,n - liczb naturalnych | a0=1
a-m=1/am
1) am∙an = am+n
2) am:an = am-n, dla a ≠ 0 i m>n 3) (am)n = am∙n 4) an∙bn = (ab)n 5) an:bn = (a:b)n, dla b ≠ 0 |
Przejdź do artykułów: |
Tablica- kolejne potęgi liczby 2, 3, 4 i 5
| n | 2n | 3n | 4n | 5n |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 2 | 4 | 9 | 16 | 25 |
| 3 | 8 | 27 | 64 | 125 |
| 4 | 16 | 81 | 256 | 625 |
| 5 | 32 | 243 | 1024 | 3125 |
| 6 | 64 | 729 | 4096 | 15625 |
| 7 | 128 | 2187 | 16384 | 78125 |
| 8 | 256 | 6561 | 65536 | 390625 |
| 9 | 512 | 19683 | 262144 | 1953125 |
| 10 | 1024 | 59049 | 1048576 | 9765625 |
| 11 | 2048 | 177147 | 4194304 | 48828125 |
| 12 | 4096 | 531441 | 16777216 | 244140625 |
| 13 | 8192 | 1594323 | 67108864 | 1220703125 |
| 14 | 16384 | 4782969 | 268435456 | 6103515625 |
| 15 | 32768 | 14348907 | 1073741824 | 30517578125 |
| 16 | 65536 | 43046721 | 4294967296 | 152587890625 |
| 17 | 131072 | 129140163 | 17179869184 | 762939453125 |
| 18 | 262144 | 387420489 | 68719476736 | 3814697265625 |
| 19 | 524288 | 1162261467 | 274877906944 | 19073486328125 |
| 20 | 1048576 | 3486784401 | 1099511627776 | 95367431640625 |
Pierwiastkowanie
| Definicja | Własności | Więcej |
|---|---|---|
Pierwiastek stopnia n z liczby a ≥ 0 oznaczamy symbolem |
Wyłączanie przed pierwiastek:
|
Przejdź do artykułów: |
Tablica - wyłączanie czynnika przed pierwiastek
Poniższa tabela zawiera te liczby, dla których z pierwiastków stopnia od 2 do 5 tych liczb można wyłączyć czynnik przed pierwiastek.
| n | √n | 3√n | 4√n | 5√n |
| 4 | 2 | |||
| 8 | 2√2 | 2 | ||
| 9 | 3 | |||
| 12 | 2√3 | |||
| 16 | 4 | 23√2 | 2 | |
| 18 | 3√2 | |||
| 20 | 2√5 | |||
| 24 | 2√6 | 23√3 | ||
| 25 | 5 | |||
| 27 | 3√3 | 3 | ||
| 28 | 2√7 | |||
| 32 | 4√2 | 23√4 | 24√2 | 2 |
| 36 | 6 | |||
| 40 | 2√10 | 23√5 | ||
| 44 | 2√11 | |||
| 45 | 3√5 | |||
| 48 | 4√3 | 23√6 | 24√3 | |
| 49 | 7 | |||
| 50 | 5√2 | |||
| 52 | 2√13 | |||
| 54 | 3√6 | 33√2 | ||
| 56 | 2√14 | 23√7 | ||
| 60 | 2√15 | |||
| 63 | 3√7 | |||
| 64 | 8 | 4 | 24√4 | 25√2 |
| 68 | 2√17 | |||
| 72 | 6√2 | 23√9 | ||
| 75 | 5√3 | |||
| 76 | 2√19 | |||
| 80 | 4√5 | 23√10 | 24√5 | |
| 81 | 9 | 33√3 | 3 | |
| 84 | 2√21 | |||
| 88 | 2√22 | 23√11 | ||
| 90 | 3√10 | |||
| 92 | 2√23 | |||
| 96 | 4√6 | 23√12 | 24√6 | 25√3 |
| 98 | 7√2 | |||
| 99 | 3√11 | |||
| 100 | 10 | |||
| 104 | 2√26 | 23√13 | ||
| 108 | 6√3 | 33√4 | ||
| 112 | 4√7 | 23√14 | 24√7 | |
| 116 | 2√29 | |||
| 117 | 3√13 | |||
| 120 | 2√30 | 23√15 | ||
| 121 | 11 | |||
| 124 | 2√31 | |||
| 125 | 5√5 | 5 | ||
| 126 | 3√14 | |||
| 128 | 8√2 | 43√2 | 24√8 | 25√4 |
| 132 | 2√33 | |||
| 135 | 3√15 | 33√5 | ||
| 136 | 2√34 | 23√17 | ||
| 140 | 2√35 | |||
| 144 | 12 | 23√18 | 24√9 | |
| 147 | 7√3 | |||
| 148 | 2√37 | |||
| 150 | 5√6 | |||
| 152 | 2√38 | 23√19 | ||
| 153 | 3√17 | |||
| 156 | 2√39 | |||
| 160 | 4√10 | 23√20 | 24√10 | 25√5 |
| 162 | 9√2 | 33√6 | 34√2 | |
| 164 | 2√41 | |||
| 168 | 2√42 | 23√21 | ||
| 169 | 13 | |||
| 171 | 3√19 | |||
| 172 | 2√43 | |||
| 175 | 5√7 | |||
| 176 | 4√11 | 23√22 | 24√11 | |
| 180 | 6√5 | |||
| 184 | 2√46 | 23√23 | ||
| 188 | 2√47 | |||
| 189 | 3√21 | 33√7 | ||
| 192 | 8√3 | 43√3 | 24√12 | 25√6 |
| 196 | 14 | |||
| 198 | 3√22 | |||
| 200 | 10√2 | 23√25 |
Logarytm
| Definicja | Własności | Więcej |
|---|---|---|
Logarytmem liczby x>0 przy podstawie a, gdzie a>0 i a≠1 nazywamy wykładnik potęgi, do której należy podnieść liczbę a, aby otrzymać liczbę x.
Logarytm o podstawie 10 nazywamy logarytmem dziesiętnym.
Logarytm naturalny liczby x jest to logarytm po podstawie równej e=2,718281828... (liczba Eulera) i oznaczamy go przez ln x | dla
|
Przejdź do artykułów: |
 Liczby pierwsze
Liczby pierwsze
Tablica 1999 kolejnych liczb pierwszych, uszeregowanych według kolejności ich występowania w formie wygodnej tablicy.
Analiza matematyczna
Ciąg arytmetyczny
| Definicja | Własności | Więcej |
|---|---|---|
Ciąg (an) jest ciągiem arytmetycznym, jeżeli istnieje liczba r, że dla każdego n w przypadku ciągu nieskończonego i dla każdego n<k w przypadku ciągu skończonego, k-wyrazowego oraz k≥3 spełniony jest warunek: Liczba r to tak zwana różnica ciągu arytmetycznego. | Różnica ciągu arytmetycznego:
Wzór na n-ty wyraz ciągu:
Suma n kolejnych wyrazów ciągu arytmetycznego: |
Przejdź do artykułu Ciąg arytmetyczny. |
Ciąg geometryczny
| Definicja | Własności | Więcej |
|---|---|---|
Ciąg (an) jest ciągiem geometrycznym, jeżeli istnieje liczba q≠0, że dla każdego n w przypadku ciągu nieskończonego i dla każdego n<k w przypadku ciągu skończonego, k-wyrazowego oraz k≥3 spełniony jest warunek: Liczbę q to tak zwany iloraz ciągu geometrycznego. | Iloraz ciągu geometrycznego:
Wzór na n-ty wyraz ciągu:
Inne:
Wzór na sumę n początkowych wyrazów ciągu geometrycznego: 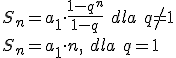 |
Przejdź do artykułu Ciąg geometryczny. |
Szereg geometryczny
| Definicja | Własności | Więcej |
|---|---|---|
Ciąg (Sn) nazywamy szeregiem geometrycznym lub ciągiem sum częściowych ciągu geometrycznego. Ponieważ n-ty wyraz ciągu geometrycznego wyraża się wzorem | Szereg geometryczny jest zbieżny , gdy |q|<1 i ma sumę natomiast jest rozbieżny, gdy |
Przejdź do artykułu: Szereg geometryczny. |
Geometria
 Objętości brył
Objętości brył
Wykaz wzorów na objętość najbardziej brył takich jak sześcian, prostopadłościan, walec, stożek, kula, i innych.
 Figury foremne
Figury foremne
Wykaz długości promienia okręgu wpisanego i opisanego na wielokącie foremnym oraz pola powierzchni wielokątów foremnych.
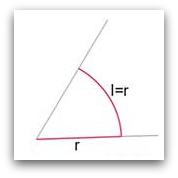 Miary kątów
Miary kątów
Tabela zawiera miary stopniowe i łukowe najczęściej spotykanych kątów w kursach matematyki.
Tablice trygonometryczne
 Wartości funkcji trygonometrycznych
Wartości funkcji trygonometrycznych
Tablica wartości funkcji trygonometrycznych dla najczęściej stosowanych miar kątów.
Wykaz wszystkich podstawowych wzorów (tożsamości) trygonometrycznych.
Spis wzorów redukcyjnych dla funkcji sinus, cosinus, tangens i cotangens.
Kombinatoryka
Spis podstawowych wzorów z zakresu kombinatoryki.
© medianauka.pl, 2013-11-10, A-2131
Data aktualizacji artykułu: 2020-02-28

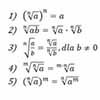
![1)\ (\sqrt[n]{a})^n=a\\ 2)\ \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\\ 3)\ \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}},\ b\neq 0\\ 4)\ \sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}\\ 5)\ (\sqrt[n]{a})^m=\sqrt[n]{a^m}](matematyka/wzory/146/1.gif)
![\sqrt[n]{a^n\cdot b}=\sqrt[n]{a^n}\cdot \sqrt[n]{b}=a\sqrt[n]{b},\ a\geq0,\ b\geq 0](matematyka/wzory/147/1.gif)
 Rozkład liczby na czynniki
Rozkład liczby na czynniki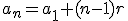
 Wzory trygonometryczne
Wzory trygonometryczne Wzory redukcyjne
Wzory redukcyjne Kombinatoryka
Kombinatoryka



