Liczby pierwsze

Co to jest liczba pierwsza i liczba złożona?

Liczba pierwsza jest to liczba naturalna większa od jedności, która ma dokładnie dwa podzielniki (jeden i samą siebie).

Liczba złożona jest to liczba naturalną większa od jedności, która nie jest liczbą pierwszą.

Ze względu na liczbę dzielników możemy więc wszystkie liczby naturalne podzielić na trzy rozłączne podzbiory zbioru liczb naturalnych:

Zbiór	Opis
{0, 1}	Liczby, które nie mają dzielnika lub posiadają jeden dzielnik.
{2, 3, 5, 7, 11, 13, ...}	Liczby, które posiadają dwa dzielniki — liczby pierwsze.
{4, 6, 8, 9, 10, 12, ...}	Liczby, które posiadają więcej niż 2 dzielniki — liczby złożone.

Ile jest liczb pierwszych? Zbiór liczb pierwszych ma nieskończenie wiele elementów.

Liczby pierwsze to jakby atomy w świecie matematyki, z których przy pomocy mnożenia można zbudować wszystkie pozostałe liczby (złożone).

Każdą liczbę złożoną można zapisać w postaci iloczynu liczb pierwszych. To tak zwany rozkład liczby na czynniki pierwsze.

Rozkład liczby na czynniki pierwsze to nic innego jak przedstawienie danej liczby w postaci iloczynu liczb pierwszych.

Przykłady

12 = 2·2·3
999 = 3·3·3·37
1971 = 3·3·3·73
126870 = 2·3·5·4229

Poniżej zamieszczamy prosty kalkulator — program sprawdzający, czy dana liczba jest liczbą pierwszą, czy złożoną i czy da się rozłożyć na czynniki.

Kalkulator
W tym miejscu możesz rozłożyć dowolną liczbę naturalną na czynniki pierwsze. Pamiętaj, aby podać liczbę naturalną. Jeżeli podasz liczbę rzeczywistą, do obliczeń zostanie wzięta jedynie jej część całkowita.

Wpisz liczbę naturalną:

Wynik to:

Rodzaje liczb pierwszych

Liczby pierwsze bliźniacze to takie liczby pierwsze, które różnią się o 2. Jest to więc para liczb p i p+2, gdzie p jest liczbą pierwszą. Przykłady liczb pierwszych bliźniaczych: 3 i 5, 5 i 7, 11 i 13, 71 i 73 itp.

Liczby pierwsze czworacze to liczby: p, p+2, p+6, p+8, gdzie p jest liczbą pierwszą. Są to na przykład liczby 5, 7, 11, 13.

Liczby palindromicznie pierwsze to liczby pierwsze, które czyta się tak samo od lewej, jak i od prawej strony. Są to na przykład liczby 11, 101, 131, 191, 929, 10601.

Ciekawostki

Szukanie liczb pierwszych może być intratnym zajęciem. Electronic Frontier Foundation ufundowała nagrodę za odkrycie kolejnej największej liczby pierwszej. Jak dotąd największa odkryta liczba pierwsza to 2^77232917-1 (2018 rok). Liczba ta w zapisie dziesiętnym ma ponad 23 miliony cyfr.
Możesz też wziąć udział w wyszukiwaniu kolejnych liczb pierwszych, przyłączając się do projektu GIMPS (Great Internet Mersenne Prime Search) poprzez udostępnienie mocy obliczeniowej swojego komputera. Szczegóły w języku angielskim znajdziesz tutaj.

Pytania

Ile dzielników ma trzecia potęga liczby pierwszej?

Trzecia potęga dowolnej liczby pierwszej p ma 4 dzielniki:
p⁰ = 1
p¹ = p
p² = p·p
p³ = p·p·p

Na przykład 2³= 8 ma dzielniki 1, 2, 4 i 8.

Jaka jest najmniejsza liczba pierwsza?

Najmniejszą liczbą pierwszą jest liczba 2.

Jaka jest najmniejsza nieparzysta liczba pierwsza?

Jest to liczba 3.

Czy 1 jest liczbą pierwszą?

Nie.

Jakie są dwucyfrowe liczby pierwsze?

Wszystkie liczby pierwsze dwucyfrowe to: 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Czy istnieją liczby naturalne, które nie są ani pierwsze, ani złożone?

Tak. Są to liczby 0 i 1.

Czy istnieją parzyste liczby pierwsze?

Tak. Jest to liczba 2.

Jaka jest najmniejsza liczba złożona?

To liczba 4.

Czy istnieje wzór na liczby pierwsze?

Jak do tej pory nie poznaliśmy takiego wzoru. Z rozmieszczeniem liczb pierwszych na osi wiąże się jedna z największych zagadek matematyki — hipoteza Riemanna. Rozwiązanie tego problemu ma duże znaczenie dla matematyki, statystyki i fizyki. Trwają prace naukowe na całym świecie, mające na celu znalezienie wspólnego mianownika między rozmieszczeniem liczb pierwszych, a bardzo podobnymi zależnościami w świecie subatomowym. Może jest to klucz do zagadki budowy samego Wszechświata? Polecamy rewelacyjny film o naturze liczb pierwszych.

Lista liczb pierwszych

Poniższa tabela zawiera pierwsze 999 liczb pierwszych. Poniżej kilka słów tytułem wyjaśnienia, jak należy z niej korzystać.

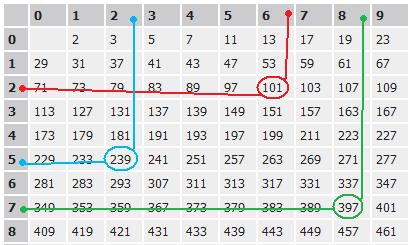
tablice

Na czerwono zaznaczono liczbę 101. Jest to liczba pierwsza. Aby odczytać, którą z kolei jest liczbą pierwszą, liczbę dziesiątek odczytujemy z pierwszej kolumny, liczbę jedności z pierwszego rzędu. Zatem 101 jest 26 liczbą pierwszą. Analogicznie: liczba 239 jest 52 z kolei liczbą pierwszą, a liczba 397 jest 78 z kolei liczbą pierwszą.

Tablica liczb pierwszych
Powyżej znajduje się instrukcja jak korzystać z poniższej tabeli.

Tablica ta zawiera kolejne liczby pierwsze. Pierwsze trzy rzędy tabeli zawierają liczby pierwsze do 100, szesnaście rzędów zawiera 1000 liczb pierwszych!

	0	1	2	3	4	5	6	7	8	9
0		2	3	5	7	11	13	17	19	23
1	29	31	37	41	43	47	53	59	61	67
2	71	73	79	83	89	97	101	103	107	109
3	113	127	131	137	139	149	151	157	163	167
4	173	179	181	191	193	197	199	211	223	227
5	229	233	239	241	251	257	263	269	271	277
6	281	283	293	307	311	313	317	331	337	347
7	349	353	359	367	373	379	383	389	397	401
8	409	419	421	431	433	439	443	449	457	461
9	463	467	479	487	491	499	503	509	521	523
10	541	547	557	563	569	571	577	587	593	599
11	601	607	613	617	619	631	641	643	647	653
12	659	661	673	677	683	691	701	709	719	727
13	733	739	743	751	757	761	769	773	787	797
14	809	811	821	823	827	829	839	853	857	859
15	863	877	881	883	887	907	911	919	929	937
16	941	947	953	967	971	977	983	991	997	1009
17	1013	1019	1021	1031	1033	1039	1049	1051	1061	1063
18	1069	1087	1091	1093	1097	1103	1109	1117	1123	1129
19	1151	1153	1163	1171	1181	1187	1193	1201	1213	1217
20	1223	1229	1231	1237	1249	1259	1277	1279	1283	1289
21	1291	1297	1301	1303	1307	1319	1321	1327	1361	1367
22	1373	1381	1399	1409	1423	1427	1429	1433	1439	1447
23	1451	1453	1459	1471	1481	1483	1487	1489	1493	1499
24	1511	1523	1531	1543	1549	1553	1559	1567	1571	1579
25	1583	1597	1601	1607	1609	1613	1619	1621	1627	1637
26	1657	1663	1667	1669	1693	1697	1699	1709	1721	1723
27	1733	1741	1747	1753	1759	1777	1783	1787	1789	1801
28	1811	1823	1831	1847	1861	1867	1871	1873	1877	1879
29	1889	1901	1907	1913	1931	1933	1949	1951	1973	1979
30	1987	1993	1997	1999	2003	2011	2017	2027	2029	2039
31	2053	2063	2069	2081	2083	2087	2089	2099	2111	2113
32	2129	2131	2137	2141	2143	2153	2161	2179	2203	2207
33	2213	2221	2237	2239	2243	2251	2267	2269	2273	2281
34	2287	2293	2297	2309	2311	2333	2339	2341	2347	2351
35	2357	2371	2377	2381	2383	2389	2393	2399	2411	2417
36	2423	2437	2441	2447	2459	2467	2473	2477	2503	2521
37	2531	2539	2543	2549	2551	2557	2579	2591	2593	2609
38	2617	2621	2633	2647	2657	2659	2663	2671	2677	2683
39	2687	2689	2693	2699	2707	2711	2713	2719	2729	2731
40	2741	2749	2753	2767	2777	2789	2791	2797	2801	2803
41	2819	2833	2837	2843	2851	2857	2861	2879	2887	2897
42	2903	2909	2917	2927	2939	2953	2957	2963	2969	2971
43	2999	3001	3011	3019	3023	3037	3041	3049	3061	3067
44	3079	3083	3089	3109	3119	3121	3137	3163	3167	3169
45	3181	3187	3191	3203	3209	3217	3221	3229	3251	3253
46	3257	3259	3271	3299	3301	3307	3313	3319	3323	3329
47	3331	3343	3347	3359	3361	3371	3373	3389	3391	3407
48	3413	3433	3449	3457	3461	3463	3467	3469	3491	3499
49	3511	3517	3527	3529	3533	3539	3541	3547	3557	3559
50	3571	3581	3583	3593	3607	3613	3617	3623	3631	3637
51	3643	3659	3671	3673	3677	3691	3697	3701	3709	3719
52	3727	3733	3739	3761	3767	3769	3779	3793	3797	3803
53	3821	3823	3833	3847	3851	3853	3863	3877	3881	3889
54	3907	3911	3917	3919	3923	3929	3931	3943	3947	3967
55	3989	4001	4003	4007	4013	4019	4021	4027	4049	4051
56	4057	4073	4079	4091	4093	4099	4111	4127	4129	4133
57	4139	4153	4157	4159	4177	4201	4211	4217	4219	4229
58	4231	4241	4243	4253	4259	4261	4271	4273	4283	4289
59	4297	4327	4337	4339	4349	4357	4363	4373	4391	4397
60	4409	4421	4423	4441	4447	4451	4457	4463	4481	4483
61	4493	4507	4513	4517	4519	4523	4547	4549	4561	4567
62	4583	4591	4597	4603	4621	4637	4639	4643	4649	4651
63	4657	4663	4673	4679	4691	4703	4721	4723	4729	4733
64	4751	4759	4783	4787	4789	4793	4799	4801	4813	4817
65	4831	4861	4871	4877	4889	4903	4909	4919	4931	4933
66	4937	4943	4951	4957	4967	4969	4973	4987	4993	4999
67	5003	5009	5011	5021	5023	5039	5051	5059	5077	5081
68	5087	5099	5101	5107	5113	5119	5147	5153	5167	5171
69	5179	5189	5197	5209	5227	5231	5233	5237	5261	5273
70	5279	5281	5297	5303	5309	5323	5333	5347	5351	5381
71	5387	5393	5399	5407	5413	5417	5419	5431	5437	5441
72	5443	5449	5471	5477	5479	5483	5501	5503	5507	5519
73	5521	5527	5531	5557	5563	5569	5573	5581	5591	5623
74	5639	5641	5647	5651	5653	5657	5659	5669	5683	5689
75	5693	5701	5711	5717	5737	5741	5743	5749	5779	5783
76	5791	5801	5807	5813	5821	5827	5839	5843	5849	5851
77	5857	5861	5867	5869	5879	5881	5897	5903	5923	5927
78	5939	5953	5981	5987	6007	6011	6029	6037	6043	6047
79	6053	6067	6073	6079	6089	6091	6101	6113	6121	6131
80	6133	6143	6151	6163	6173	6197	6199	6203	6211	6217
81	6221	6229	6247	6257	6263	6269	6271	6277	6287	6299
82	6301	6311	6317	6323	6329	6337	6343	6353	6359	6361
83	6367	6373	6379	6389	6397	6421	6427	6449	6451	6469
84	6473	6481	6491	6521	6529	6547	6551	6553	6563	6569
85	6571	6577	6581	6599	6607	6619	6637	6653	6659	6661
86	6673	6679	6689	6691	6701	6703	6709	6719	6733	6737
87	6761	6763	6779	6781	6791	6793	6803	6823	6827	6829
88	6833	6841	6857	6863	6869	6871	6883	6899	6907	6911
89	6917	6947	6949	6959	6961	6967	6971	6977	6983	6991
90	6997	7001	7013	7019	7027	7039	7043	7057	7069	7079
91	7103	7109	7121	7127	7129	7151	7159	7177	7187	7193
92	7207	7211	7213	7219	7229	7237	7243	7247	7253	7283
93	7297	7307	7309	7321	7331	7333	7349	7351	7369	7393
94	7411	7417	7433	7451	7457	7459	7477	7481	7487	7489
95	7499	7507	7517	7523	7529	7537	7541	7547	7549	7559
96	7561	7573	7577	7583	7589	7591	7603	7607	7621	7639
97	7643	7649	7669	7673	7681	7687	7691	7699	7703	7717
98	7723	7727	7741	7753	7757	7759	7789	7793	7817	7823
99	7829	7841	7853	7867	7873	7877	7879	7883	7901	7907
100	7919	7927	7933	7937	7949	7951	7963	7993	8009	8011
101	8017	8039	8053	8059	8069	8081	8087	8089	8093	8101
102	8111	8117	8123	8147	8161	8167	8171	8179	8191	8209
103	8219	8221	8231	8233	8237	8243	8263	8269	8273	8287
104	8291	8293	8297	8311	8317	8329	8353	8363	8369	8377
105	8387	8389	8419	8423	8429	8431	8443	8447	8461	8467
106	8501	8513	8521	8527	8537	8539	8543	8563	8573	8581
107	8597	8599	8609	8623	8627	8629	8641	8647	8663	8669
108	8677	8681	8689	8693	8699	8707	8713	8719	8731	8737
109	8741	8747	8753	8761	8779	8783	8803	8807	8819	8821
110	8831	8837	8839	8849	8861	8863	8867	8887	8893	8923
111	8929	8933	8941	8951	8963	8969	8971	8999	9001	9007
112	9011	9013	9029	9041	9043	9049	9059	9067	9091	9103
113	9109	9127	9133	9137	9151	9157	9161	9173	9181	9187
114	9199	9203	9209	9221	9227	9239	9241	9257	9277	9281
115	9283	9293	9311	9319	9323	9337	9341	9343	9349	9371
116	9377	9391	9397	9403	9413	9419	9421	9431	9433	9437
117	9439	9461	9463	9467	9473	9479	9491	9497	9511	9521
118	9533	9539	9547	9551	9587	9601	9613	9619	9623	9629
119	9631	9643	9649	9661	9677	9679	9689	9697	9719	9721
120	9733	9739	9743	9749	9767	9769	9781	9787	9791	9803
121	9811	9817	9829	9833	9839	9851	9857	9859	9871	9883
122	9887	9901	9907	9923	9929	9931	9941	9949	9967	9973
123	10007	10009	10037	10039	10061	10067	10069	10079	10091	10093
124	10099	10103	10111	10133	10139	10141	10151	10159	10163	10169
125	10177	10181	10193	10211	10223	10243	10247	10253	10259	10267
126	10271	10273	10289	10301	10303	10313	10321	10331	10333	10337
127	10343	10357	10369	10391	10399	10427	10429	10433	10453	10457
128	10459	10463	10477	10487	10499	10501	10513	10529	10531	10559
129	10567	10589	10597	10601	10607	10613	10627	10631	10639	10651
130	10657	10663	10667	10687	10691	10709	10711	10723	10729	10733
131	10739	10753	10771	10781	10789	10799	10831	10837	10847	10853
132	10859	10861	10867	10883	10889	10891	10903	10909	10937	10939
133	10949	10957	10973	10979	10987	10993	11003	11027	11047	11057
134	11059	11069	11071	11083	11087	11093	11113	11117	11119	11131
135	11149	11159	11161	11171	11173	11177	11197	11213	11239	11243
136	11251	11257	11261	11273	11279	11287	11299	11311	11317	11321
137	11329	11351	11353	11369	11383	11393	11399	11411	11423	11437
138	11443	11447	11467	11471	11483	11489	11491	11497	11503	11519
139	11527	11549	11551	11579	11587	11593	11597	11617	11621	11633
140	11657	11677	11681	11689	11699	11701	11717	11719	11731	11743
141	11777	11779	11783	11789	11801	11807	11813	11821	11827	11831
142	11833	11839	11863	11867	11887	11897	11903	11909	11923	11927
143	11933	11939	11941	11953	11959	11969	11971	11981	11987	12007
144	12011	12037	12041	12043	12049	12071	12073	12097	12101	12107
145	12109	12113	12119	12143	12149	12157	12161	12163	12197	12203
146	12211	12227	12239	12241	12251	12253	12263	12269	12277	12281
147	12289	12301	12323	12329	12343	12347	12373	12377	12379	12391
148	12401	12409	12413	12421	12433	12437	12451	12457	12473	12479
149	12487	12491	12497	12503	12511	12517	12527	12539	12541	12547
150	12553	12569	12577	12583	12589	12601	12611	12613	12619	12637
151	12641	12647	12653	12659	12671	12689	12697	12703	12713	12721
152	12739	12743	12757	12763	12781	12791	12799	12809	12821	12823
153	12829	12841	12853	12889	12893	12899	12907	12911	12917	12919
154	12923	12941	12953	12959	12967	12973	12979	12983	13001	13003
155	13007	13009	13033	13037	13043	13049	13063	13093	13099	13103
156	13109	13121	13127	13147	13151	13159	13163	13171	13177	13183
157	13187	13217	13219	13229	13241	13249	13259	13267	13291	13297
158	13309	13313	13327	13331	13337	13339	13367	13381	13397	13399
159	13411	13417	13421	13441	13451	13457	13463	13469	13477	13487
160	13499	13513	13523	13537	13553	13567	13577	13591	13597	13613
161	13619	13627	13633	13649	13669	13679	13681	13687	13691	13693
162	13697	13709	13711	13721	13723	13729	13751	13757	13759	13763
163	13781	13789	13799	13807	13829	13831	13841	13859	13873	13877
164	13879	13883	13901	13903	13907	13913	13921	13931	13933	13963
165	13967	13997	13999	14009	14011	14029	14033	14051	14057	14071
166	14081	14083	14087	14107	14143	14149	14153	14159	14173	14177
167	14197	14207	14221	14243	14249	14251	14281	14293	14303	14321
168	14323	14327	14341	14347	14369	14387	14389	14401	14407	14411
169	14419	14423	14431	14437	14447	14449	14461	14479	14489	14503
170	14519	14533	14537	14543	14549	14551	14557	14561	14563	14591
171	14593	14621	14627	14629	14633	14639	14653	14657	14669	14683
172	14699	14713	14717	14723	14731	14737	14741	14747	14753	14759
173	14767	14771	14779	14783	14797	14813	14821	14827	14831	14843
174	14851	14867	14869	14879	14887	14891	14897	14923	14929	14939
175	14947	14951	14957	14969	14983	15013	15017	15031	15053	15061
176	15073	15077	15083	15091	15101	15107	15121	15131	15137	15139
177	15149	15161	15173	15187	15193	15199	15217	15227	15233	15241
178	15259	15263	15269	15271	15277	15287	15289	15299	15307	15313
179	15319	15329	15331	15349	15359	15361	15373	15377	15383	15391
180	15401	15413	15427	15439	15443	15451	15461	15467	15473	15493
181	15497	15511	15527	15541	15551	15559	15569	15581	15583	15601
182	15607	15619	15629	15641	15643	15647	15649	15661	15667	15671
183	15679	15683	15727	15731	15733	15737	15739	15749	15761	15767
184	15773	15787	15791	15797	15803	15809	15817	15823	15859	15877
185	15881	15887	15889	15901	15907	15913	15919	15923	15937	15959
186	15971	15973	15991	16001	16007	16033	16057	16061	16063	16067
187	16069	16073	16087	16091	16097	16103	16111	16127	16139	16141
188	16183	16187	16189	16193	16217	16223	16229	16231	16249	16253
189	16267	16273	16301	16319	16333	16339	16349	16361	16363	16369
190	16381	16411	16417	16421	16427	16433	16447	16451	16453	16477
191	16481	16487	16493	16519	16529	16547	16553	16561	16567	16573
192	16603	16607	16619	16631	16633	16649	16651	16657	16661	16673
193	16691	16693	16699	16703	16729	16741	16747	16759	16763	16787
194	16811	16823	16829	16831	16843	16871	16879	16883	16889	16901
195	16903	16921	16927	16931	16937	16943	16963	16979	16981	16987
196	16993	17011	17021	17027	17029	17033	17041	17047	17053	17077
197	17093	17099	17107	17117	17123	17137	17159	17167	17183	17189
198	17191	17203	17207	17209	17231	17239	17257	17291	17293	17299
199	17317	17321	17327	17333	17341	17351	17359	17377	17383	17387

Ćwiczenia

Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.