Najmniejsza wspólna wielokrotność — NWW

Najmniejsza wspólna wielokrotność (NWW) dwóch liczb jest to najmniejsza spośród takich liczb, które są jednocześnie wielokrotnościami obu liczb.

Najmniejszą wielokrotność dwóch liczb a i b oznaczamy w następujący sposób: NWW(a, b).

Przykłady

Wielokrotnościami liczby 4 są liczby: 8, 12, 16, 20, 24, 28, ...
Wielokrotnościami liczby 3 są liczby: 6, 9, 12, 15, 18, 21, 24, ...

Liczba 12, 24,... są wspólnymi wielokrotnościami liczb 3 i 4, a 12 jest z nich wielokrotnością najmniejszą.

Zapisujemy to w następujący sposób: NWW(3, 4) = 12.

NWW dwóch liczb naturalnych znajdujemy, wykorzystując rozkład na czynniki pierwsze.

NWW jest równa iloczynowi jednej z danych liczb i wszystkich czynników pierwszych rozkładu drugiej liczby, które nie występowały w rozkładzie na czynniki pierwszej liczby. Ilustruje to poniższa animacja:

Animacja

Przykład

Znaleźć najmniejszą wspólną wielokrotność liczb 999 i 3108.

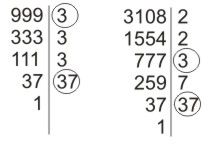
NWW (999,3108) = 999·2·2·7 = 3108·3·3 = 27972

Uwaga: NWW to najmniejsza, a nie największa wspólna wielokrotność, jak można czasem usłyszeć ze szkolnych ławek.

Kalkulator NWW

Poniższy program online znajduje NWW dwóch liczb. Wspomaga samodzielne obliczanie NWW poprzez możliwość porównania wyniku.

Kalkulator — nww
Podaj dowolne dwie liczby naturalne. Nasz robot znajdzie rozwiązanie.

Wpisz dane:

Liczba 1:
Liczba 2:

Rozwiązanie:

Pytania

Jak obliczyć NWW w inny sposób?

Jeżeli znamy liczbę NWD (największy wspólny dzielnik), to w łatwy sposób obliczymy NWW, czyli najmniejszą wspólną wielokrotność liczb a i b, korzystając ze wzoru: NWW (a, b) = ab / NWD (a, b).

Zadania z rozwiązaniami

Zadanie nr 1.

Znaleźć najmniejszą wspólną wielokrotność NWW liczb: a) 168 i 762, b) 3125 i 625, c) 2016 i 33264, d) 432, 112 i 84.

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Podzielność liczb

Liczby pierwsze

Rozkład liczby na czynniki pierwsze

Największy wspólny dzielnik NWD

Zaokrąglanie liczb

Właściwości liczb rzeczywistych