Rozkład liczby na czynniki pierwsze

Rozkład liczby naturalnej na czynniki pierwsze polega na jej przedstawieniu w postaci iloczynu liczb pierwszych.

Każdą liczbę złożoną można przedstawić w postaci iloczynu liczb pierwszych. Oto kilka przykładów:

Przykłady

Rozłóż podane liczby na czynniki pierwsze:

12 = 2·2·3
999 = 3·3·3·37
1971 = 3·3·3·73
126870 = 2·3·5·4229

Pisemny rozkład liczby na czynniki pierwsze

Rozkład liczby na czynniki pierwsze bardzo często wykorzystujemy w matematyce. Warto poznać pisemny sposób rozkładu, który został zilustrowany poniższą animacją:

Aby pisemnie rozłożyć liczbę na czynniki pierwsze, zapisujemy ją po lewej stronie pionowej kreski, a po prawej najmniejszy dzielnik, będący liczbą pierwszą. Wykonujemy dzielenie, wynik zapisujemy po lewej stronie i czynność tę powtarzamy tak długo, aż w wyniku kolejnego dzielenia otrzymamy jeden. Iloczyn wszystkich liczb zapisanych w kolumnie po prawej stronie kreski będzie równy danej liczbie.

Przykłady

A oto dwa inne przykłady rozkładu liczb naturalnych:

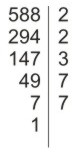
588 = 2·2·3·7·7;

Poniżej pisemny rozkład liczby 588.

rozkład na czynniki pierwsze - przykład 1
600 = 2·2·2·3·5·5;

Poniżej pisemny rozkład liczby 600.

rozkład na czynniki pierwsze - przykład 2

Kalkulator

W tym miejscu możesz rozłożyć dowolną liczbę naturalną na czynniki pierwsze. Pamiętaj, aby podać liczbę naturalną. Jeżeli podasz liczbę rzeczywistą, do obliczeń zostanie wzięta jedynie jej część całkowita.

Wpisz liczbę naturalną:

Wynik to: