Iloraz
Czym jest iloraz i dzielenie?
Dzielenie jest jednym z czterech podstawowych działań arytmetycznych.
Iloraz jest to wynik dzielenia.
Symbol dzielenia
Stosujemy różne symbole dla oznaczenia dzielenia: „:”, „/”, „÷”, a także kreskę ułamkową w ułamku zwykłym.
Dzielna i dzielnik
Dzielna jest to liczba, którą dzielimy przez drugą liczbę.
Dzielnik jest to liczba, przez którą dzielimy pierwszą liczbę. Dzielnik jest różny od zera.

W działaniu \(a:b=c\) mamy \(b\neq 0\).
Oznacza to, że dzielenie przez zero jest niewykonalne.
Liczba odwrotna
Przykłady
| Liczba | Odwrotność |
|---|---|
| 2 | \(\frac{1}{2}\) |
| 1 | 1 |
| 0 | - |
| \(\frac{1}{3}\) | 3 |
| 0,3 | \(\frac{10}{3}\) |
| \(10^{-1}\) | 10 |
Własności dzielenia
Dzielenie jest działaniem odwrotnym do mnożenia. Oznacza to, że \(a\cdot \frac{1}{a} = 1\). Pamiętamy przy tym, że 1 jest elementem neutralnym iloczynu.
Dzielenie nie jest przemienne, a więc \(a:b \neq b:a\).
Dzielenie nie jest łączne, a więc \((a:b):c \neq a:(b:c)\).
Dzielenie z resztą
Każda liczba całkowita \(a\) może być przedstawiona w postaci sumy iloczynu ilorazu \(q\) przez dzielnik \(d\) różny od zera oraz reszty \(r\).
gdzie \(0\leq r < |d|\).
Przykłady
\(12:2= 5 \ reszta\ 2\), bo \(2\cdot 5+2=12\)
\(5:2= 1 \ reszta\ 1\), bo \(2\cdot 2+1=5\)
\(33:4= 8 \ reszta\ 1\), bo \(4\cdot 8+1=33\)
Tabliczka dzielenia
Tabliczka dzielenia do druku w postaci karty pracy z zakresu do 100 w formacie PDF znajduje się poniżej.
Pytania
Dlaczego dzielenie przez zero nie jest wykonalne?
Zauważmy najpierw, że \(a/b=c \Leftrightarrow a=b\cdot c\) (gdyż dzielenie jest działaniem odwrotnym do iloczynu).
Załóżmy, że dzielnik może być zerem, a więc \(a=0\cdot c\).
Rozpatrzy dwa przypadki:
1) Jeżeli \(a=0\), wówczas \(0=0\cdot c\) , więc \(c\) może być dowolną liczbą. Działanie nie jest jednoznaczne.
2) Jeżeli \(a\neq 0\) wówczas \(0\cdot c=a (\neq 0)\) i zauważamy, że nie istnieje taka liczba \(c\), która spełnia ten warunek.
Dzielenie przez zero nie jest zatem wykonalne.
Czy liczba odwrotna i przeciwna to jest to samo?
Nie. Liczba przeciwna do \(a\) to \(-a\), a odwrotna to \(\frac{1}{a}\).
Wykonujemy najpierw mnożenie czy dzielenie?
Jeżeli w danym wyrażeniu algebraicznym nie występują nawiasy, to kolejność wykonywania działań jest następująca:
- potęgowanie i pierwiastkowanie,
- mnożenie i dzielenie w kolejności ich występowania,
- dodawanie i odejmowanie również w kolejności ich występowania.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy \(\frac{4}{7}\), a jeżeli do licznika i do mianownika dodamy \(1\), to otrzymamy \(\frac{1}{2}\). Wyznacz ten ułamek.

Zadanie nr 2.
Wskaż resztę z dzielenia
A. 45:11
B. 1:2
C. 111:21
D. 78:3
E. 0:3

Zadanie nr 3.
Wyznacz liczby odwrotne do podanych
A. \(1\)
B. \(\frac{4}{11}\)
C. \(-66\)
D. \(10^{-1}\)
E. \(0,125\)
F. \(\sqrt{7}\)
G. \(\pi +1\)
Wybrane karty pracy
Powiązane materiały
© medianauka.pl, 2009-01-10, A-132
Data aktualizacji artykułu: 2023-03-09





 Podzielność liczb
Podzielność liczb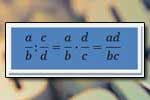 Dzielenie ułamków zwykłych
Dzielenie ułamków zwykłych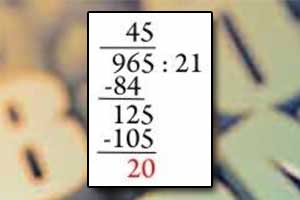 Dzielenie pisemne
Dzielenie pisemne Dzielenie (iloraz)
Dzielenie (iloraz) Rozkład liczby na czynniki pierwsze
Rozkład liczby na czynniki pierwsze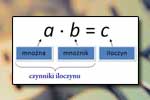 Iloczyn
Iloczyn