Dzielenie ułamków
Jak się dzieli ułamki zwykłe? Iloraz dwóch ułamków zwykłych obliczamy według poniższego wzoru:
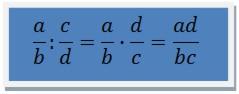
Zauważ, że dzielenie ułamków zwykłych o różnych mianownikach odbywa się tak samo, jak dzielenie ułamków o różnych mianownikach.
Przykłady
A oto przykłady zastosowania powyższego wzoru:
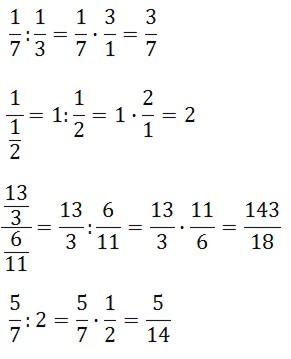
Kalkulator
Nasz program online rozwiązuje dowolne zadanie dzielenia ułamków. Spróbuj w ramach ćwiczenia sam rozwiązać zadania dzielenia ułamków zwykłych, a potem sprawdź wyniki za pomocą naszego kalkulatora.
 Kalkulator
Kalkulator
Dzielenie ułamków zwykłych
| : | ||||
Zobacz także artykuł mnożenie ułamków zwykłych, w którym również znajdziesz kalkulator i kolejne przykłady działań na ułamkach zwykłych.
Dzielenie ułamków dziesiętnych
Dzielenie ułamków dziesiętnych omawiamy w artykule o dzieleniu pisemnym.
Zadania z rozwiązaniami

Zadanie nr 1.
Oblicz:
a) \(\frac{\frac{7}{8}:\frac{1}{4}}{\frac{21}{4}:0,75}\)
b) \(\frac{\frac{5}{4}}{\frac{5}{16}}\cdot \frac{\frac{4}{5}}{\frac{24}{50}}\)
c) \(1:\frac{1}{2}:\frac{1}{4}:\frac{1}{8}:\frac{1}{16}\)
d) \(\frac{\ \ \frac{\ \frac{1}{2} \ }{3} \ \ }{\frac{5}{6}}\)

Zadanie nr 2 — maturalne.
Dodatnie liczb \(x\) i \(y\) spełniają warunek \(2x=3y\). Wynika stąd, że wartość wyrażenia \(\frac{(x^2+y^2)}{xy}\) jest równa:
A. \(\frac{2}{3}\)
B. \(\frac{13}{6}\)
C. \(\frac{6}{13}\)
D. \(\frac{3}{2}\)
Powiązane materiały
© medianauka.pl, 2009-01-10, A-133
Data aktualizacji artykułu: 2023-03-09

 Iloraz, dzielenie
Iloraz, dzielenie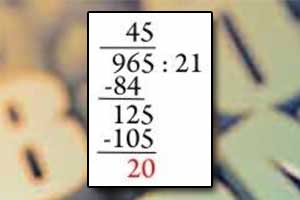 Dzielenie pisemne
Dzielenie pisemne Dzielenie (iloraz)
Dzielenie (iloraz)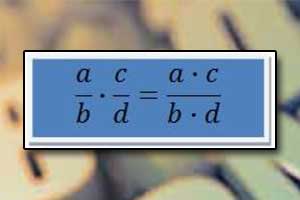 Mnożenie ułamków zwykłych
Mnożenie ułamków zwykłych