Równania i nierówności, układy równań
Postanowiliśmy wydzielić dla tematu rozwiązywania równań, nierówności oraz układów równań i nierówności osobny rozdział. Umiejętność rozwiązywania równań jest podstawową umiejętnością w matematyce. Wyróżniamy wiele typów równań i nierówności. Nasz kurs zaczynamy od podstawowych pojęć związanych z równaniami, by następnie przejść do równań liniowych z jedną niewiadomą. Dalej omawiamy coraz trudniejsze zagadnienia i typy równań. Staramy się też pokazać, w jaki sposób w praktyce można zastosować umiejętność rozwiązywania równań, nierówności i układów równań.
Równania i nierówności — zagadnienia ogólne
W tym miejscu definiujemy pojęcie równania i nierówności oraz przedstawiamy podstawowe metody ich rozwiązywania.
TESTY I ZADANIA
Równania i nierówności liniowe (pierwszego stopnia)
Równanie liniowe to równanie w postaci ax+b=c. Jest to najprostsza postać równania, mająca jednak wiele zastosowań. Badamy tu także nierówności liniowe, układy równań, wprowadzamy do równania także wartość bezwzględną.
TESTY I ZADANIA
Równania i nierówności kwadratowe (drugiego stopnia)
Równanie kwadratowe to równanie w postaci ax2+bx+c=0, gdzie a,b,c są dowolnymi liczbami rzeczywistymi oraz a jest różne od zera. To jedno z ważniejszych równań w matematyce, mające niezwykle wiele zastosowań w praktyce.
TESTY I ZADANIA
Równania i nierówności algebraiczne (wielomianowe)
Równanie algebraiczne jest to równanie w postaci W(x) = 0, gdzie W(x) oznacza wielomian.
TESTY I ZADANIA
Równania i nierówności wykładnicze i logarytmiczne
Równanie wykładnicze to takie równanie, w którym niewiadoma występuje tylko w wykładniku potęgi. Natomiast równanie logarytmiczne to takie równanie, w którym niewiadoma występuje pod znakiem logarytmu lub w podstawie logarytmu. Analogicznie określamy nierówności tego typu.
TESTY I ZADANIA
Równania i nierówności trygonometryczne
Równanie trygonometryczne to równanie, w którym niewiadoma występuje tylko w argumencie funkcji trygonometrycznej. Podobnie określamy nierówność trygonometryczną.
TESTY I ZADANIA
Równania i nierówności pozostałe
W tym miejscu omawiamy równania, nierówności i układy równań, które nie zostały opisane wyżej.
TESTY I ZADANIA
© medianauka.pl, 2016-07-08, A-3201
Data aktualizacji artykułu: 2023-01-30

 Równanie
Równanie Nierówność
Nierówność Rozwiązywanie równań
Rozwiązywanie równań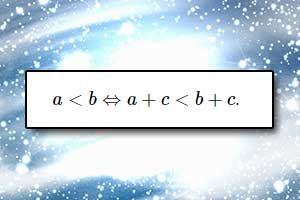 Rozwiązywanie nierówności
Rozwiązywanie nierówności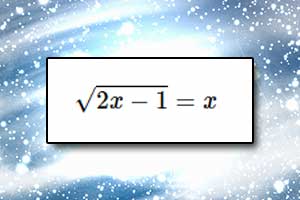 Metoda analizy starożytnych
Metoda analizy starożytnych Równanie liniowe
Równanie liniowe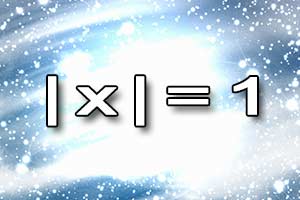 Równania z wartością bezwzględną
Równania z wartością bezwzględną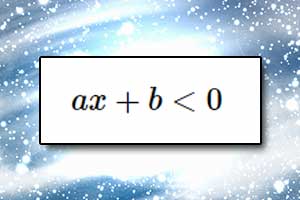 Nierówność liniowa
Nierówność liniowa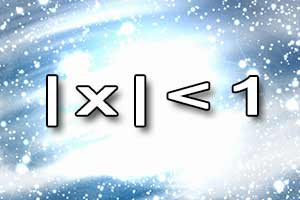 Nierówność z wartością bezwzględną
Nierówność z wartością bezwzględną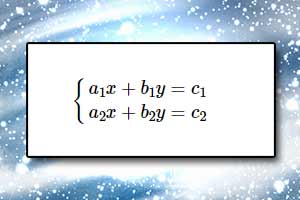 Układ równań
Układ równań Metoda wyznaczników
Metoda wyznaczników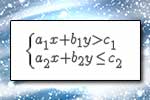 Układ nierówności pierwszego stopnia
Układ nierówności pierwszego stopnia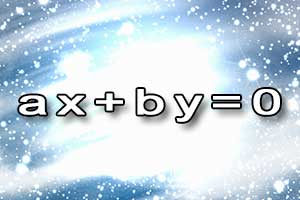 Równanie I stopnia z dwiema niewiadomymi
Równanie I stopnia z dwiema niewiadomymi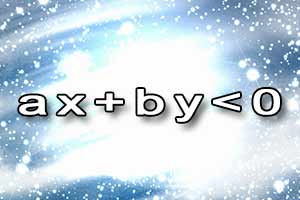 Nierówność I stopnia z dwiema niewiadomymi
Nierówność I stopnia z dwiema niewiadomymi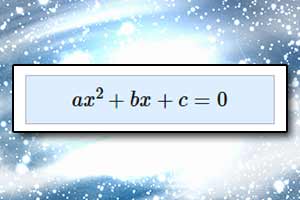 Równanie kwadratowe
Równanie kwadratowe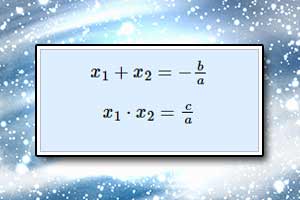 Wzory Viete'a
Wzory Viete'a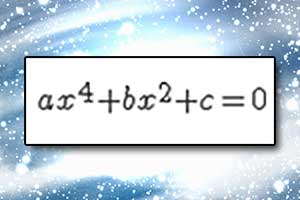 Równanie dwukwadratowe
Równanie dwukwadratowe Równanie kwadratowe z parametrem
Równanie kwadratowe z parametrem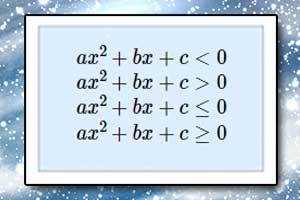 Nierówność kwadratowa
Nierówność kwadratowa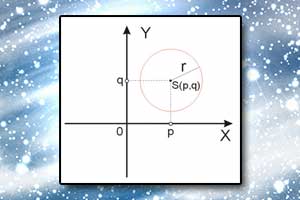 Równanie kanoniczne okręgu
Równanie kanoniczne okręgu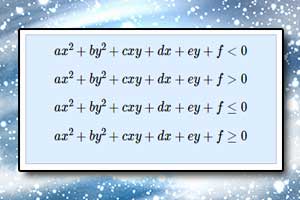 Nierówność kwadratowa z dwiema niewiadomymi
Nierówność kwadratowa z dwiema niewiadomymi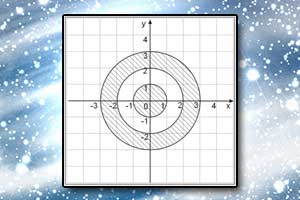 Układ równań i nierówności II stopnia
Układ równań i nierówności II stopnia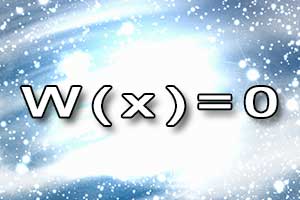 Równanie algebraiczne
Równanie algebraiczne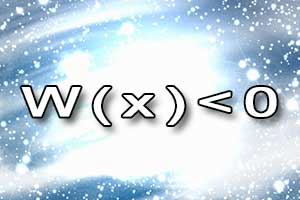 Nierówność algebraiczna
Nierówność algebraiczna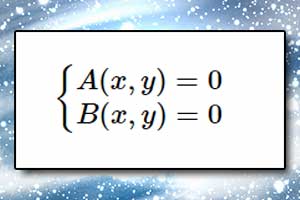 Układ równań algebraicznych
Układ równań algebraicznych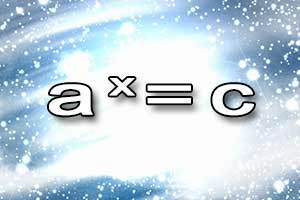 Równanie wykładnicze
Równanie wykładnicze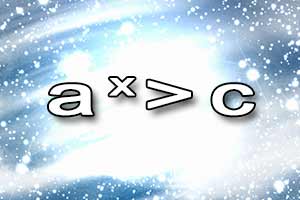 Nierówność wykładnicza
Nierówność wykładnicza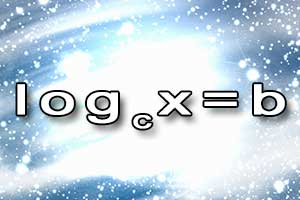 Równanie logarytmiczne
Równanie logarytmiczne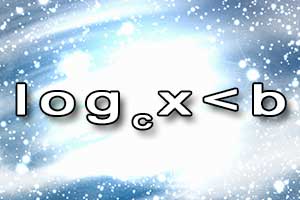 Nierówność logarytmiczna
Nierówność logarytmiczna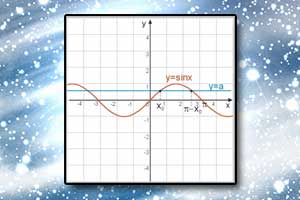 Równania trygonometryczne
Równania trygonometryczne Rozwiązywanie równań trygonometrycznych
Rozwiązywanie równań trygonometrycznych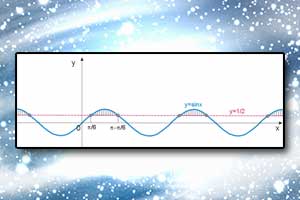 Nierówności trygonometryczne
Nierówności trygonometryczne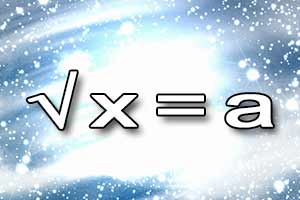 Równanie pierwiastkowe
Równanie pierwiastkowe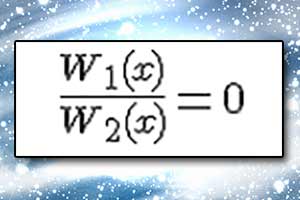 Równanie wymierne
Równanie wymierne



